This tutorial is a part of the Data Structures and Algorithms class:
- What is code complexity?
- Why is it important to measure code complexity?
- How to calculate Time and Space complexity?
- Big O complexity is asymptotic analysis
- Popular Big O complexities: names and graphs
What is code complexity?
Code compexity is a function that shows how much more CPU/RAM needed to run an algorithm, when input size of the algorithm increases. Example: complexity = n^2 + 2n + 1, where n is the input size.
Code complexity is usually used to compare algorithms. A more efficient algorithm is an algorithm that produces the same correct result with less CPU run time (Time) and less memory (Space). Example: n + 1 is more efficent than n^2 + 2n + 3.
Why is it important to measure code complexity?
It's important to measure and optimize the compexity of the code because:
- the code that works in
developmentenvironment with small input size might not work at all inproductionenvironment with large input size. So we need to know the complexity and always try to optimize. - to save CPU/RAM cost.
- to reduce wait time for a result of an algorithm.
Example: write 2 algorithms to calulate Fibonacci number at position n:
- Fibonacci sequence:
F = 0, 1, 1, 2, 3, 5, 8, 13, ... f(0) = 0f(1) = 1f(2) = f(0) + f(1) = 1- ...
f(n) = f(n-1) + f(n-2), example:fib(6) = 8
console.time('compute fib optimized time')
const fib = (n) => {
let fn_2 = 0 // f(0)
let fn_1 = 1 // f(1)
if(n === 0) return fn_2
if(n === 1) return fn_1
let fn = 0
for(let i = 2; i <= n; i++) {
fn = fn_1 + fn_2 // f(n) = f(n-1) + f(n-2)
fn_2 = fn_1
fn_1 = fn
}
return fn
}
console.log(fib(50)) // 12586269025
console.timeEnd('compute fib optimized time') // compute fib optimized time: 4.926ms$ node fib_optimized.js
12586269025
compute fib optimized time: 4.926msconsole.time('compute fib not optimized time')
const fib = (n) => {
if(n === 1) return 1
if(n === 0) return 0
return fib(n-1) + fib(n-2)
}
console.log(fib(40)) // 102334155
console.timeEnd('compute fib not optimized time') // compute fib not optimized time: 1213.639ms$ node fib_not_optimized.js
102334155
compute fib not optimized time: 1213.639ms| n | fib(n) |
fib(n) optimized O(n) |
fib(n) not optimized O(2^n) |
|---|---|---|---|
| 10 | 55 | 3.572ms ok | 5.080ms ok |
| 20 | 6765 | 4.229ms ok | 7.078ms ok |
| 30 | 832040 | 4.447ms ok | 18.584ms ok |
| 40 | 102334155 | 4.527ms ok | 1,213.639ms slow |
| 50 | 12586269025 | 4.738ms ok | 148,677.852ms useless |
| 60 | 1548008755920 | 4.885ms ok | - - - app crashed |
| . . . | . . . | . . . | |
| 1000 | 4.346655e+208 | 4.926ms ok | - - - app crashed |
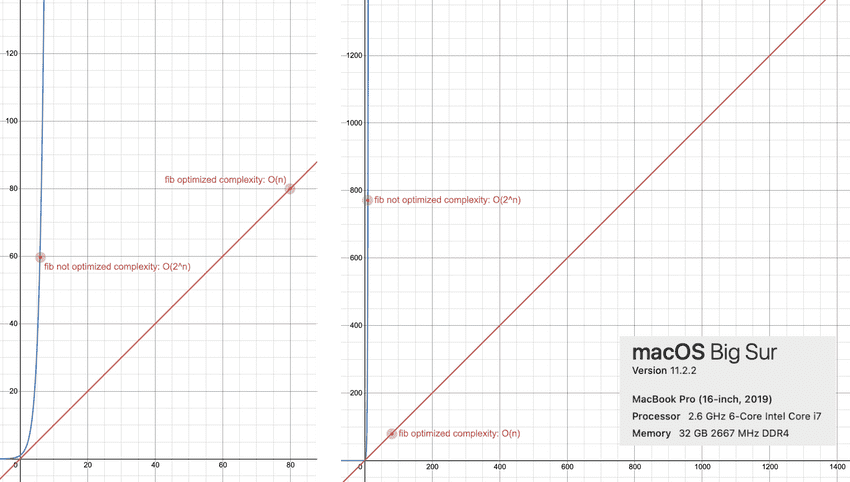
⬆️ Sample run time table for fib optimized and not optimized algorithms
⬆️ Code complexity comparison, O(2^n) vs. O(n), in small (left) and large input size
Two algorithms to calculate f(n), with input size above 50:
fib_not_optimized.jsalgorithm is useless.fib_optimized.jsalgorithm works fine.
This is why measuring and optimizing code complexity is extremely important.
How to calculate Time and Space complexity?
Line-by-line analysis:
- Time complexity: count 1 "time" for each line of code the computer runs.
- Space complexity: count 1 "space" for each variable/array element created.
- Sum up after counting.
const arr = [3, 4, 5] // array length n = 3
/*
Input: array of numbers
Process: add 1 to every single element of input array
Output: array with elements increased by 1
*/
const increase1 = (arr) => { // arr.length = n
const one = 1 // Time: 1, Space: 1
const newArr = [] // Time: 1, Space: _
for (let i = 0; i < arr.length; i++) { // Time: n, Space: 1
newArr[i] = arr[i] + one // Time: n, Space: n
}
return newArr // Time: 1, Space: 0
} // Total -------------------------------
// Time: 2n + 3, Space: n + 2
console.log('increase1(arr):', increase1(arr)) // increase1(arr): [ 4, 5, 6 ]// same correctness, more efficient
const increase2 = (arr) => {
for (let i = 0; i < arr.length; i++) { // Time: n, Space: 1
arr[i] += 1 // Time: n, Space: 0
}
return arr // Time: 1, Space: 0
} // Total -------------------------------
// Time: 2n + 1, Space: 1
console.log('increase2(arr):', increase2(arr)) // increase2(arr): [ 4, 5, 6 ]$ node increase.js
increase1(arr): [ 4, 5, 6 ]
increase2(arr): [ 4, 5, 6 ]Big O complexity is asymptotic analysis
Big O (pronounce: "Big Oh") is an asymptotic analysis of the line-by-line analysis. Asymptotic analysis means: always assume that input size is very large and highest-order term is good enough to represent the complexity. So in Big O, we take line-by-line analysis and we:
- remove lower-order terms (example:
2n^2+ 4n + 100 - remove constant factors (example:
2n^2)
Example: line by line analysis: 2n^2 + 4n + 100 -> Big O analysis: O(n^2)
⬆️ Big O complexity is asymptotic analysis
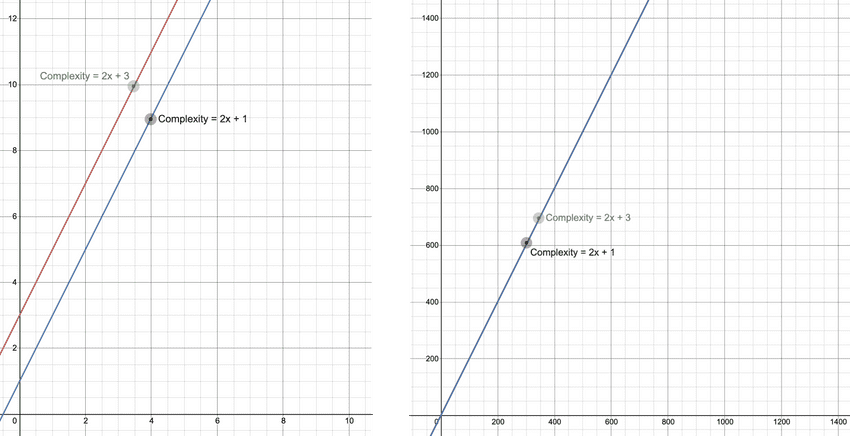
Big O analysis of increase.js algorithms:
| Algorithm | Line by line analysis | Big O analysis |
|---|---|---|
increase1 Time |
2n + 3 |
O(n) |
increase2 Time |
2n + 1 |
O(n) |
increase1 Space |
n + 2 |
O(n) |
increase2 Space |
1 |
O(1) more efficient! |
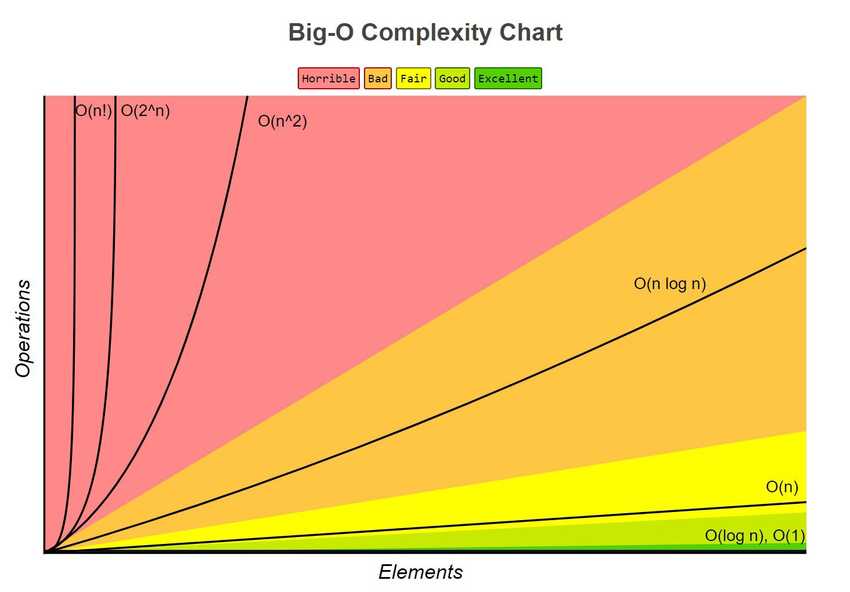
Popular Big O complexities: names and graphs
| Line by line complexities | Big O complexity | Common name | |
|---|---|---|---|
| 1 | 1,000,000 |
O(1) |
constant |
| 2 | 8logn + 10000 |
O(logn) |
|
| 3 | 3n + 2logn + 3 |
O(n) |
linear |
| 4 | 5nlogn + 2n + 5logn + 1 |
O(nlogn) |
|
| 5 | 2n^2 + 3n + 2logn + 7 |
O(n^2) |
quadratic |
| 6 | 2^n + 2n^2 + 3n + 2logn + 7 |
O(2^n) |
|
| 7 | 9n! + 2^n + 2n^2 + 3n + 2logn + 7 |
O(n!) |
Complexity: (best) O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!) (worst)
Real life interview questions
- Why do we need to calculate and optimize code complexity?
- How many lines of code does Google Chrome have? How many chances does a software engineer have to crash Google Chrome if he/she does not know the complexity of his/her code?
- Show steps to calculate
fib_optimizedandfib_not_optimizedcomplexity above? - Find a pseudo code and calculate the complexity of Merge Sort algorithm?
- Find a pseudo code and calculate the complexity of Quick Sort algorithm?
- Find a pseudo code and calculate the complexity of Bubble Sort algorithm?