Tree data structure part 1/5: Tree and Binary Tree

/
fundamentals

This tutorial is a part of the Data Structures and Algorithms class:

*Prerequisite: this tutorial uses many important concepts like nodes and links presented in Linked List. If you haven't learnt about Linked List, please stop here and learn Linked List before you continue.

Tree vs. Binary Tree vs. Binary Search Tree (BST)

Tree Binary Tree Binary Search Tree (BST)
Common Data structure with nodes and links like Linked List. But unlike Linked List, a parent node can point to multiple child nodes. So tree data structure looks like a (upside down) tree. Linked List is a tree with each node has exactly one child.
Max child/node any 2 (left, right) 2 (left, right)
Constraint N/A N/A right node > left node
Extracting useful information out of tree algorithms (tree traversals) inorder, preorder, postorder, breadth first search, depth first search.
Special N/A N/A balanced BST: O(logn) insert/delete/search
Application human ancestry tree, internet browser DOM modeling, syntax parsing for a programming language ... fast search/insert application with O(logn)

trees

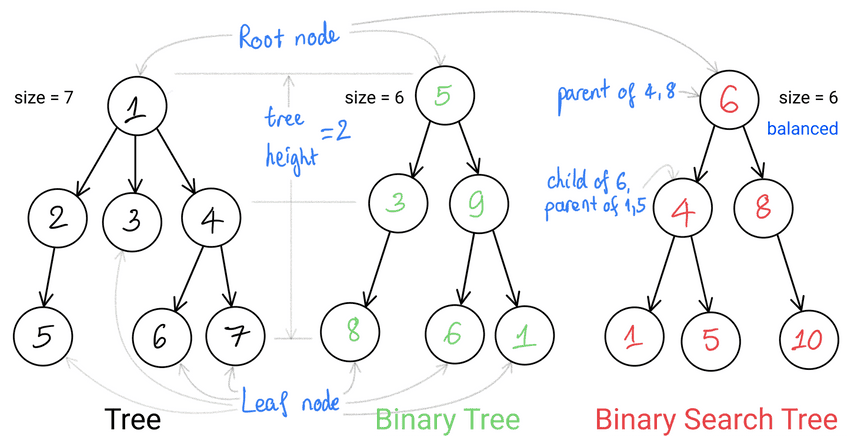
  • Tree height: distance between root to furthest leaf node, count 1 for 1 link.
  • Tree size: total number of nodes.
  • Balanced Binary Tree: left and right subtrees of every node differ in height by no more than 1.

Tree types and common properties

full complete perfect trees

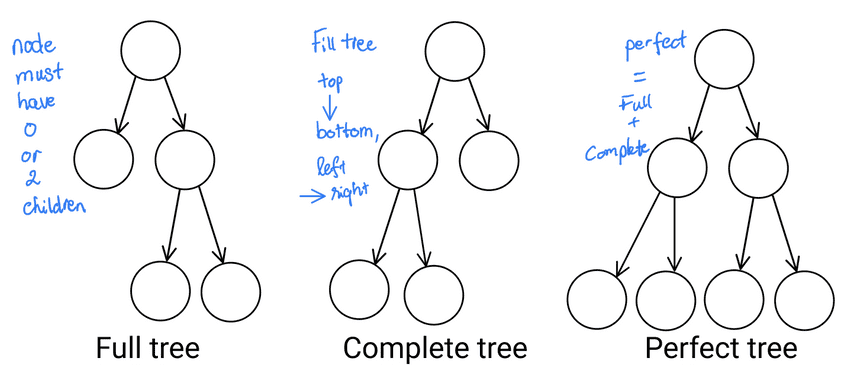
  • Full tree: every node has either 0 or 2 children
  • Complete tree: every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible, (fill order: top -> bottom, left -> right)
  • Perfect tree: all interior nodes have two children and all leaves have the same depth or same level.

Build Tree data structure

lecture-11/tree-data-structure.js
// structure of a node
class Node {
  constructor(data) {
    this.data = data
    this.children = []
  }
}

// Tree
class Tree {
  constructor(data) {
    this.root = data ? new Node(data) : null
  }
}

// create new tree
const tree = new Tree()
console.log(tree) // Tree { root: null }

// add root node, 1
tree.root = new Node(1)
console.log(JSON.stringify(tree, null, 4))

// add level 1 nodes: 2, 3, 4
tree.root.children[0] = new Node(2)
tree.root.children[1] = new Node(3)
tree.root.children[2] = new Node(4)
console.log(JSON.stringify(tree, null, 4))

// add level 2 nodes: 5, 6, 7
tree.root.children[0].children[0] = new Node(5)
tree.root.children[2].children[0] = new Node(6)
tree.root.children[2].children[1] = new Node(7)
console.log(JSON.stringify(tree, null, 4))
$ node tree-data-structure.js
Tree { root: null }
{
    "root": {
        "data": 1,
        "children": []
    }
}
{
    "root": {
        "data": 1,
        "children": [
            {
                "data": 2,
                "children": []
            },
            {
                "data": 3,
                "children": []
            },
            {
                "data": 4,
                "children": []
            }
        ]
    }
}
{
    "root": {
        "data": 1,
        "children": [
            {
                "data": 2,
                "children": [
                    {
                        "data": 5,
                        "children": []
                    }
                ]
            },
            {
                "data": 3,
                "children": []
            },
            {
                "data": 4,
                "children": [
                    {
                        "data": 6,
                        "children": []
                    },
                    {
                        "data": 7,
                        "children": []
                    }
                ]
            }
        ]
    }
}

Build Binary Tree data structure

lecture-11/binary-tree-data-structure.js
// structure of a node
class Node {
  constructor(data) {
    this.data = data
    this.left = null
    this.right = null
  }
}

// Binary Tree
class BinaryTree {
  constructor(data) {
    this.root = data ? new Node(data) : null
  }
}

// create new binary tree
const binaryTree = new BinaryTree()
console.log(binaryTree) // BinaryTree { root: null }

// add root node, 5
binaryTree.root = new Node(5)
console.log(JSON.stringify(binaryTree, null, 4))

// add level 1 nodes: 3, 9
binaryTree.root.left = new Node(3)
binaryTree.root.right = new Node(9)
console.log(JSON.stringify(binaryTree, null, 4))

// add level 2 nodes: 8, 6, 1
binaryTree.root.left.left = new Node(8)
binaryTree.root.right.left = new Node(6)
binaryTree.root.right.right = new Node(1)
console.log(JSON.stringify(binaryTree, null, 4))
$ node binary-tree-data-structure.js
BinaryTree { root: null }
{
    "root": {
        "data": 5,
        "left": null,
        "right": null
    }
}
{
    "root": {
        "data": 5,
        "left": {
            "data": 3,
            "left": null,
            "right": null
        },
        "right": {
            "data": 9,
            "left": null,
            "right": null
        }
    }
}
{
    "root": {
        "data": 5,
        "left": {
            "data": 3,
            "left": {
                "data": 8,
                "left": null,
                "right": null
            },
            "right": null
        },
        "right": {
            "data": 9,
            "left": {
                "data": 6,
                "left": null,
                "right": null
            },
            "right": {
                "data": 1,
                "left": null,
                "right": null
            }
        }
    }
}

Real life interview questions

  1. What is a balanced/unbalanced binary tree?
  2. Is a complete tree a balanced tree?
  3. Is a balanced tree a complete tree?
  4. Write your own tree data structure and add this data to your tree.
  5. Write your own binary tree data structure and add this data to your tree.
  6. Write a function to take in a binary tree and output the tree height.
  7. Given an array as a flatten version of a binary tree: root = [3,9,5,null,2,15,7], 3 is root node, 9, 5 are 1st layer nodes, null, 2, 15, 7 are 2nd layer nodes. Construct the binary tree.
  8. Solve Leetcode #112: Path Sum.