*Prerequisite: Tree data structure part 1/5: Tree and Binary Tree.
This tutorial is a part of the Data Structures and Algorithms class:
- Binary Search Tree (BST) properties
- Binary Search Tree (BST) without self-balancing mechanism
- Binary Search Tree (BST) with self-balancing mechanism
- Build Binary Search Tree (BST) data structure
Binary Search Tree (BST) properties
- Node
constraint: max2child nodes +left node<parent node<right node Insert: smaller -> go left, bigger -> go right. Farthest left node is min, farthest right node is max.Search: drop a side of the tree in each iterationDelete=search+unlink+link.
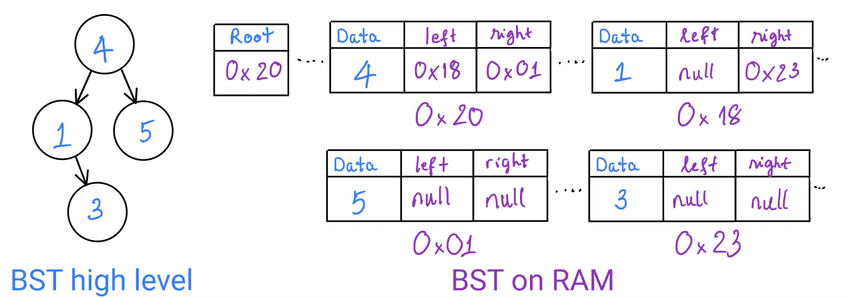
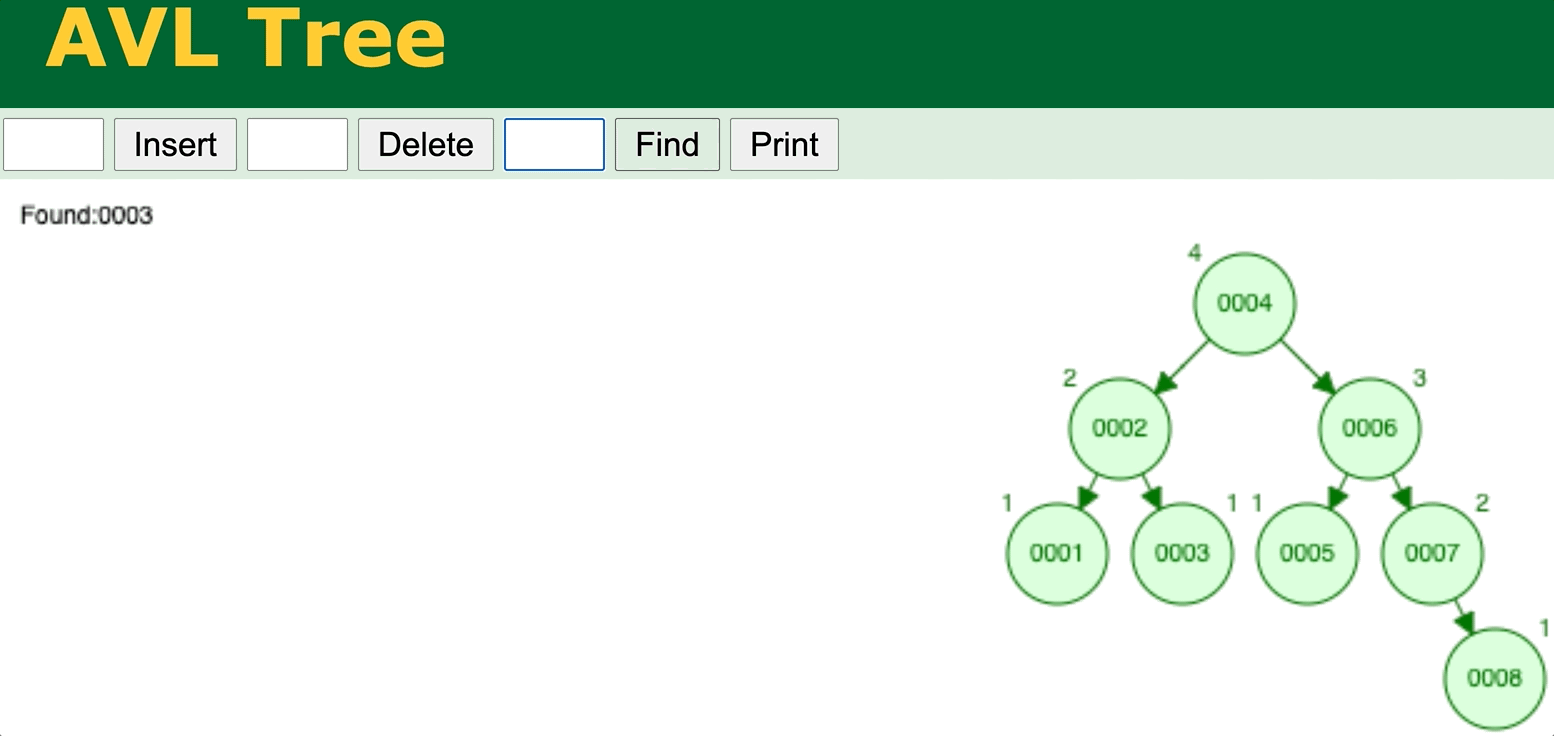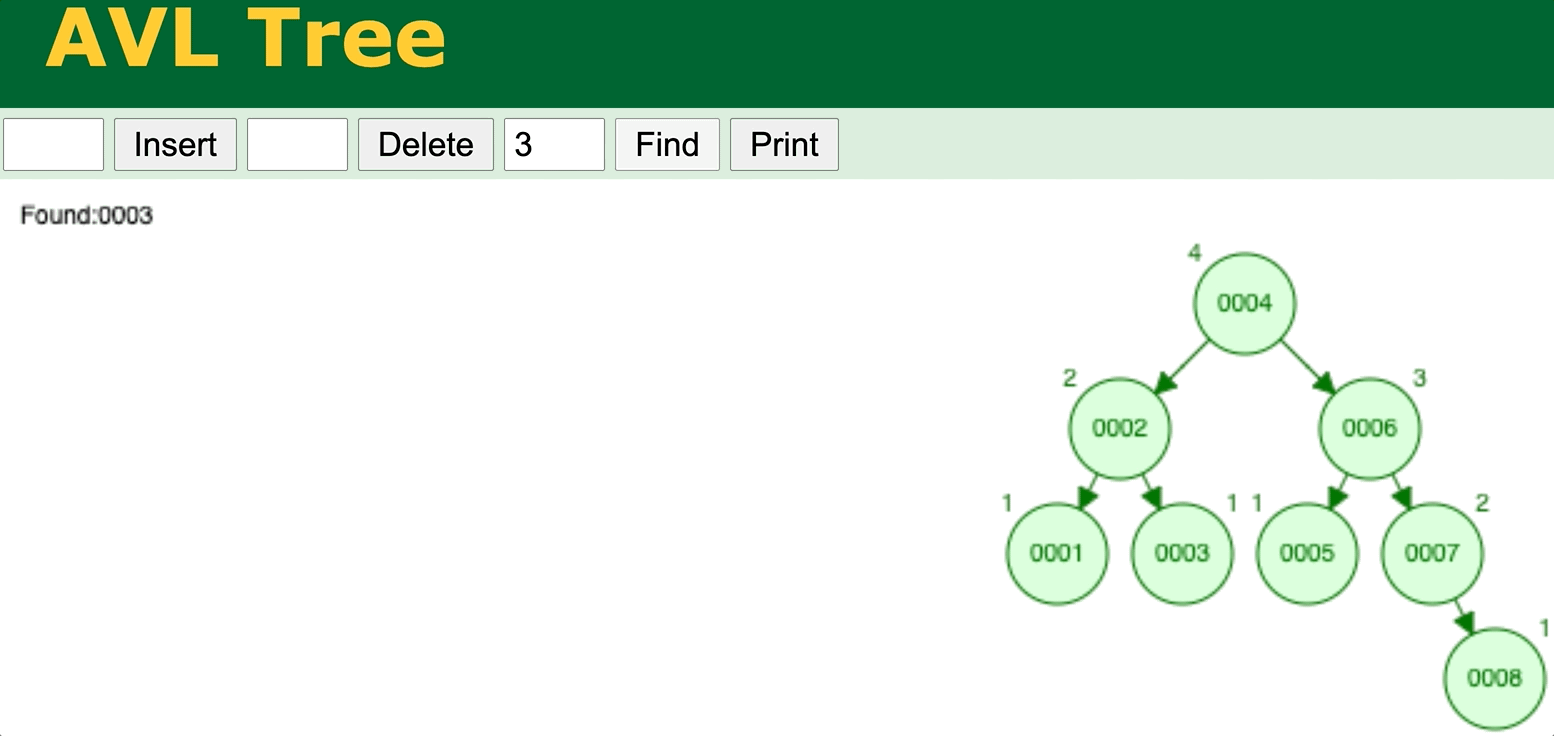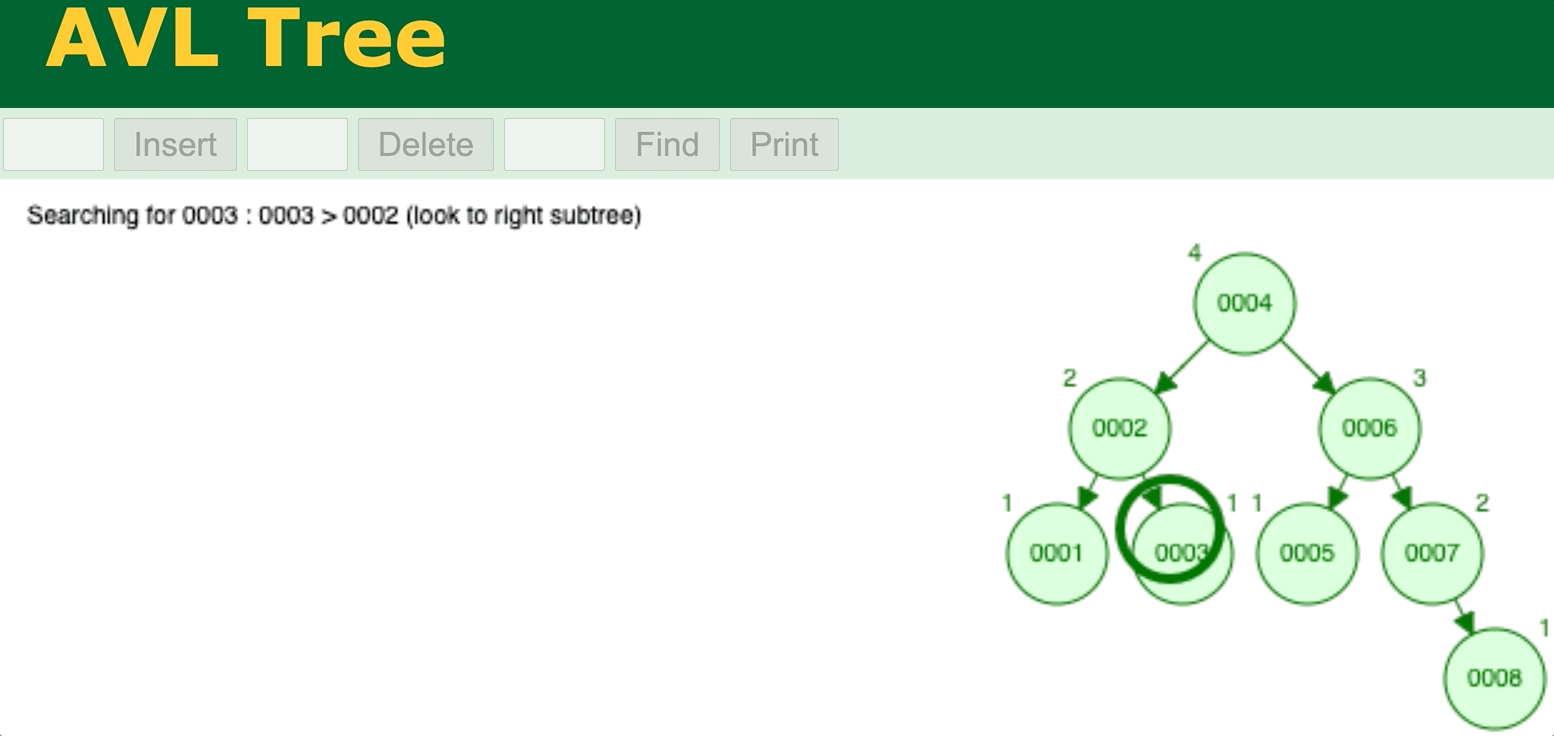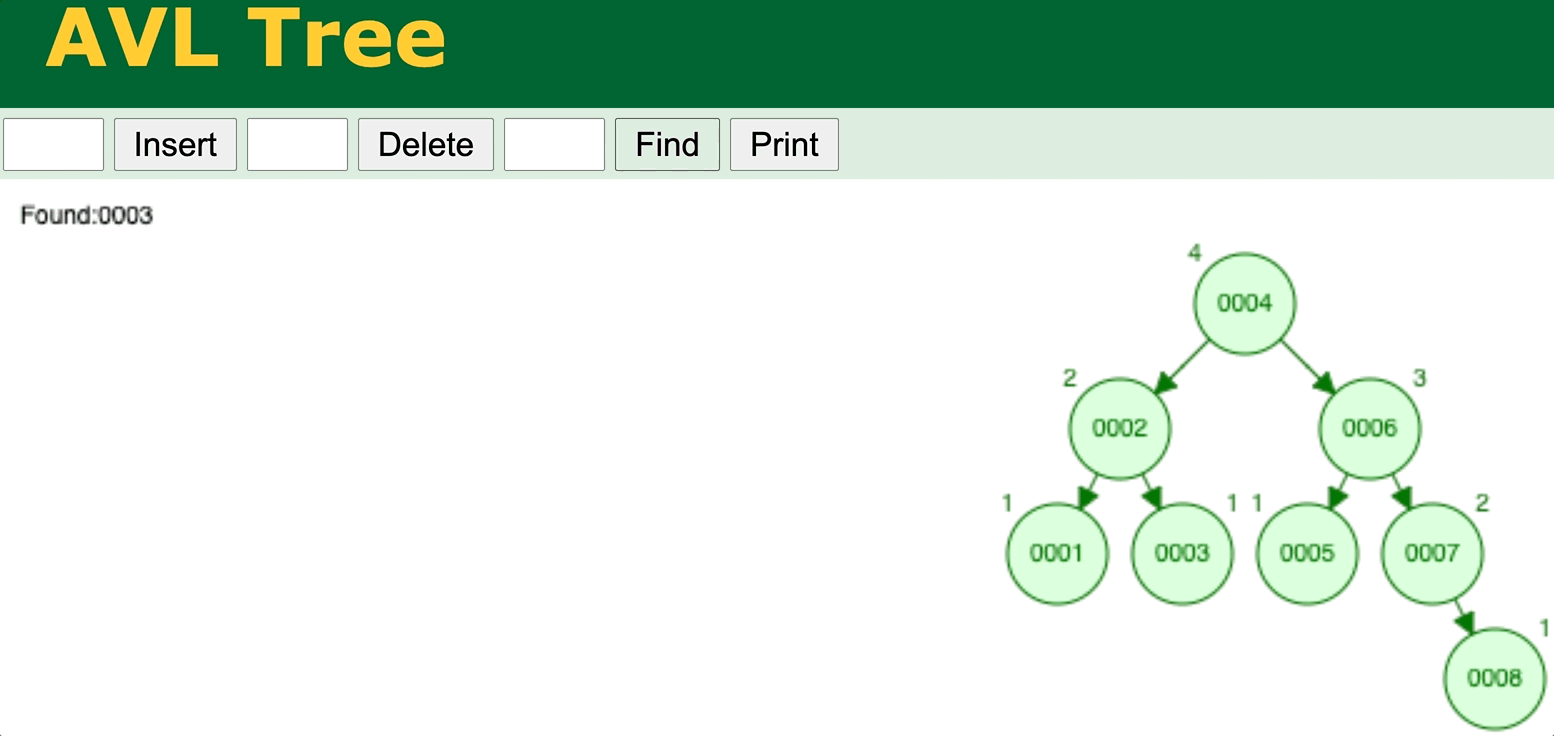
⬆️ BST/AVL Tree search operation. Try it yourself
Binary Search Tree (BST) without self-balancing mechanism
- The order of node
insertion/deletiondecides the shape of the tree. - Will become unbalanced after one (or a few)
insert/deleteoperation(s). - In the worst case scenario, BST looks like a Linked List.
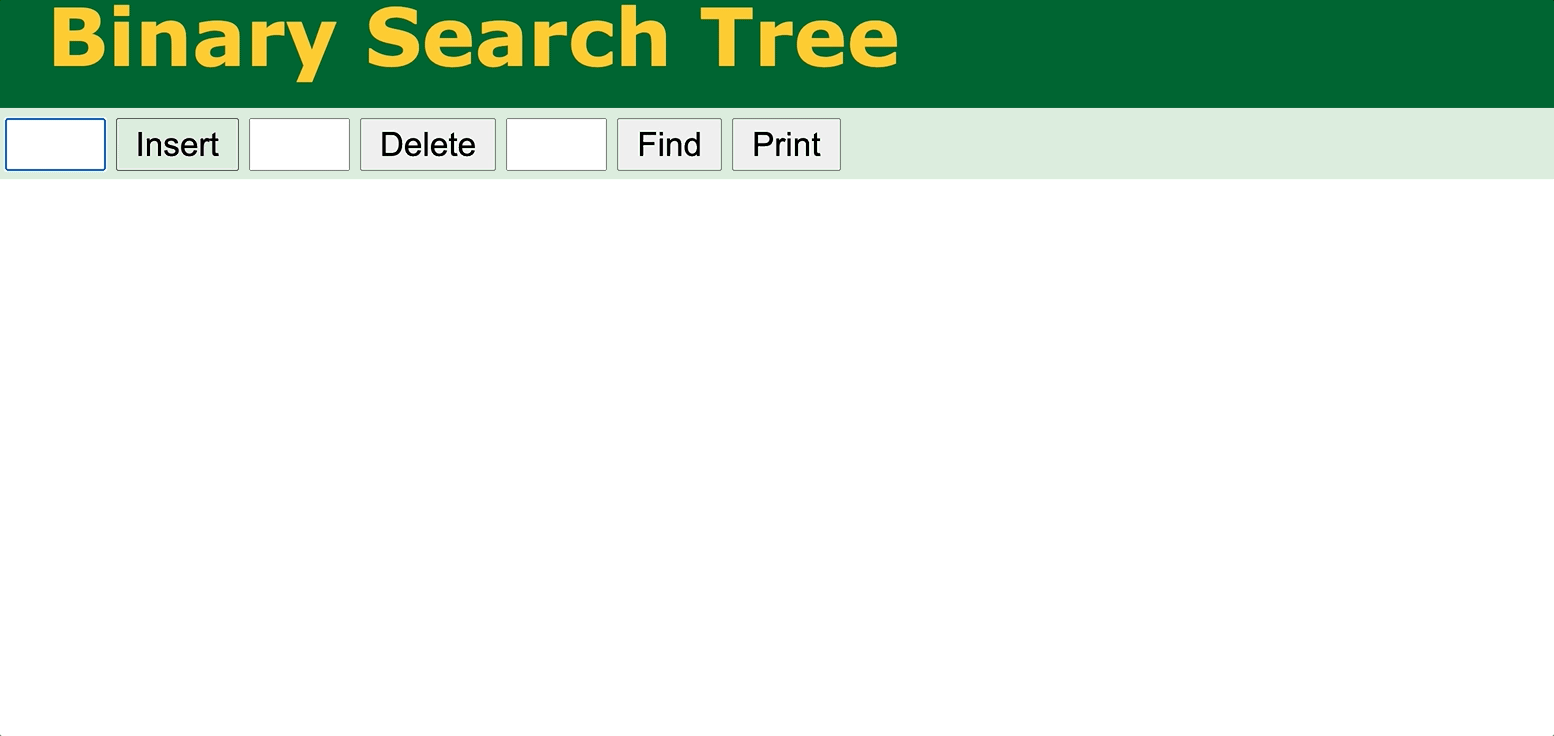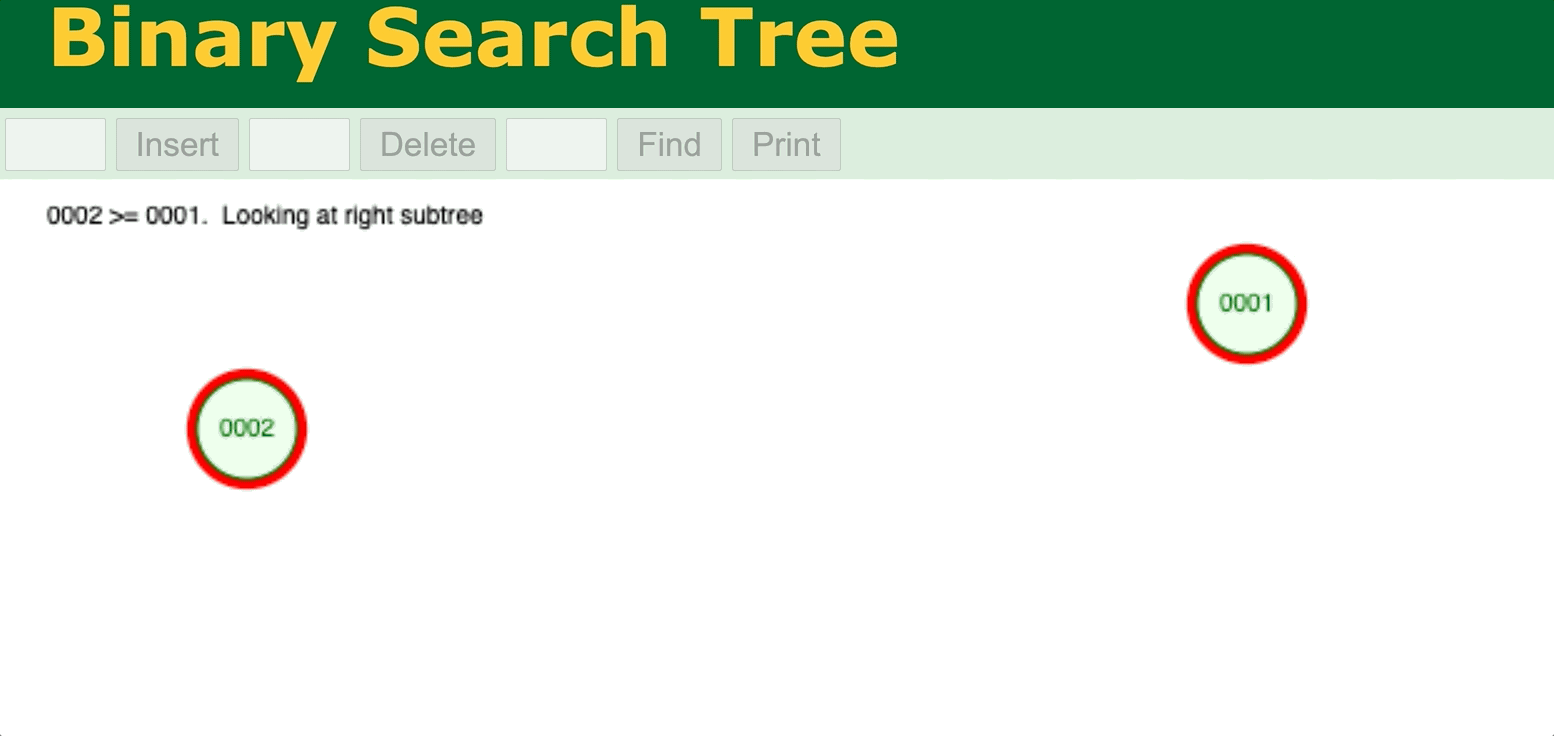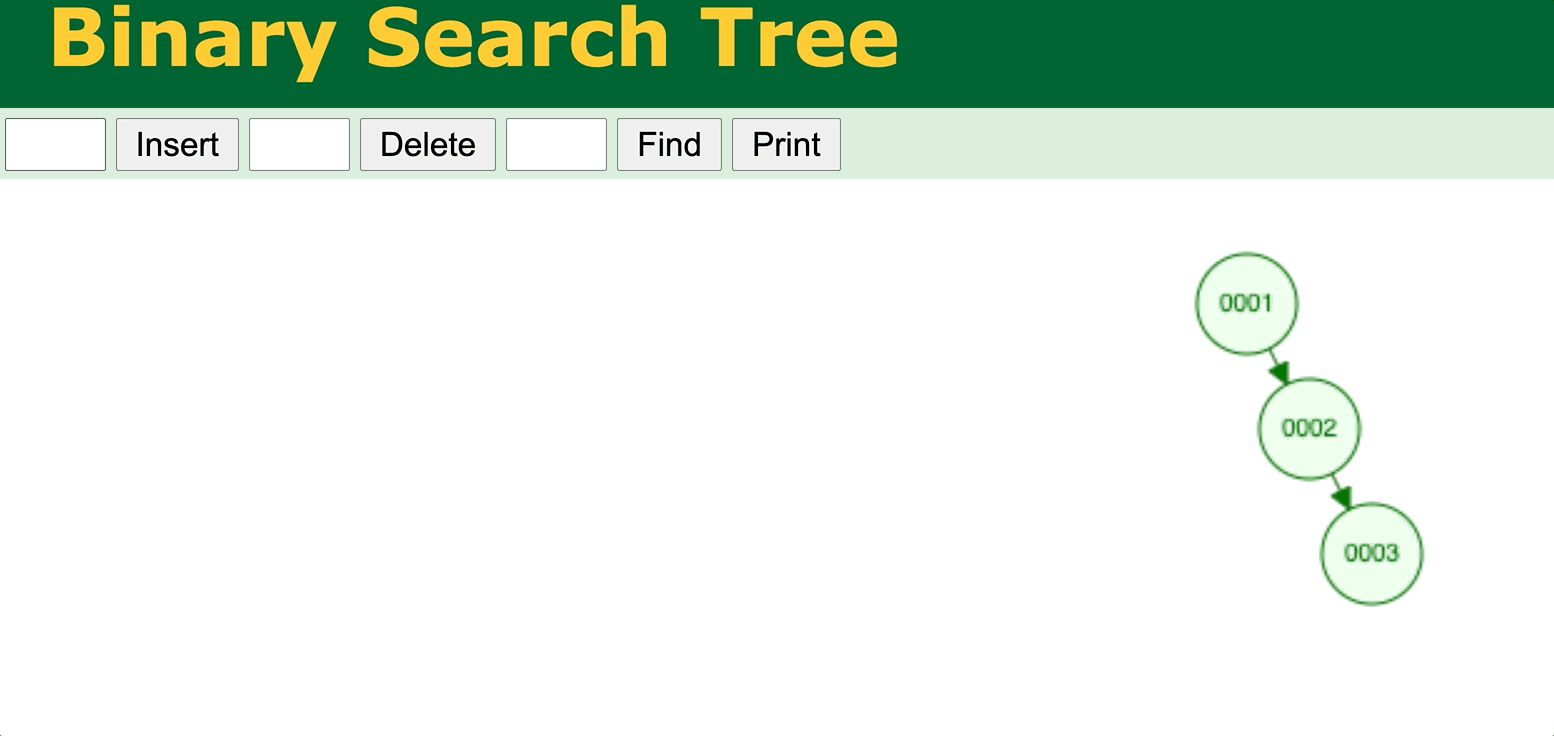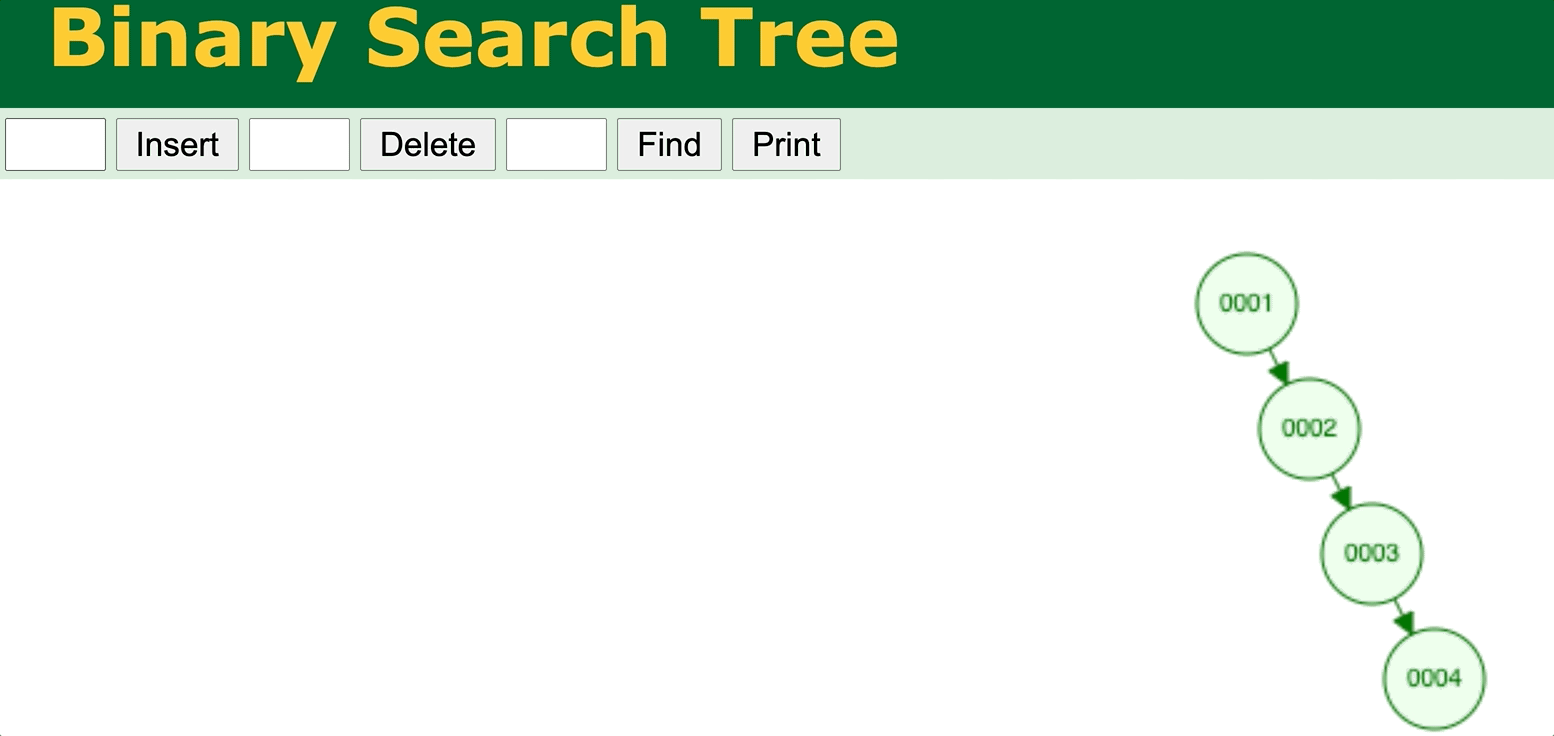
⬆️ Binary Search Tree data insertion without self-balancing 1 (worst case). Try it yourself
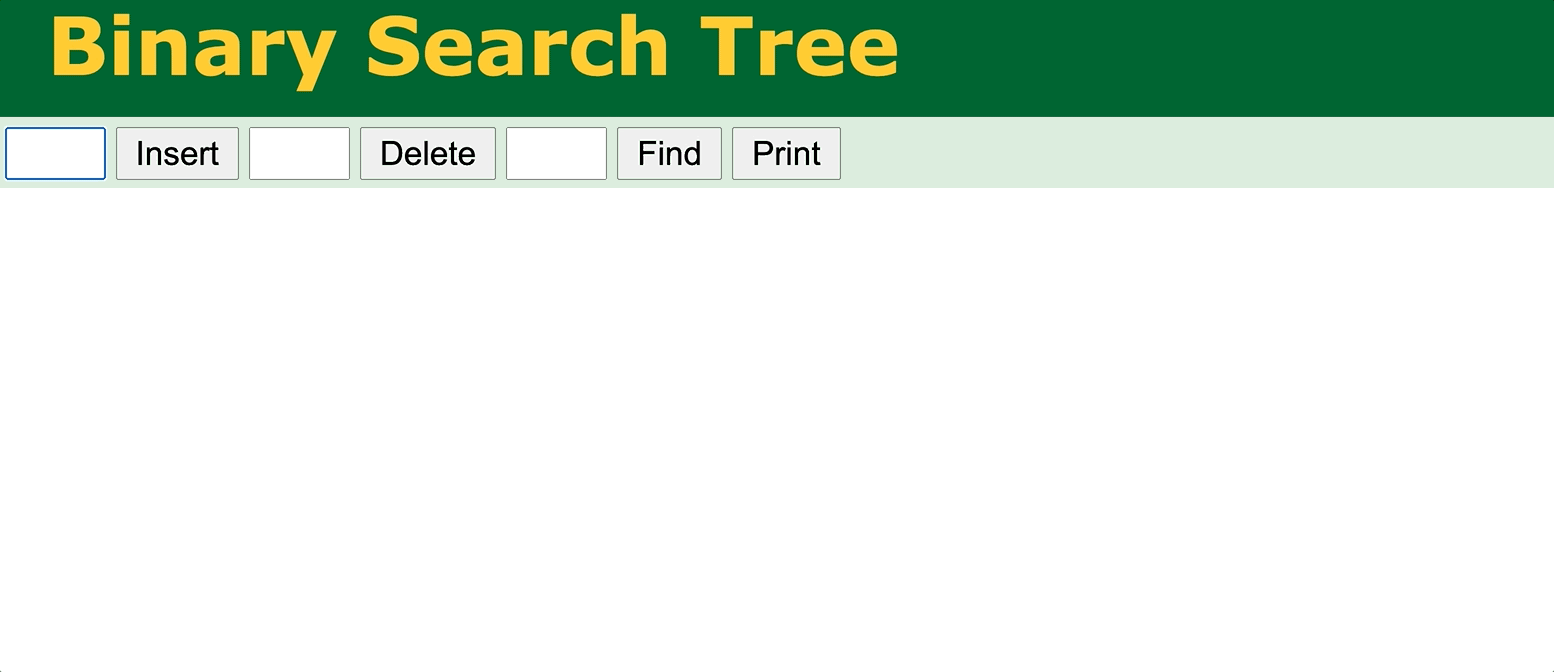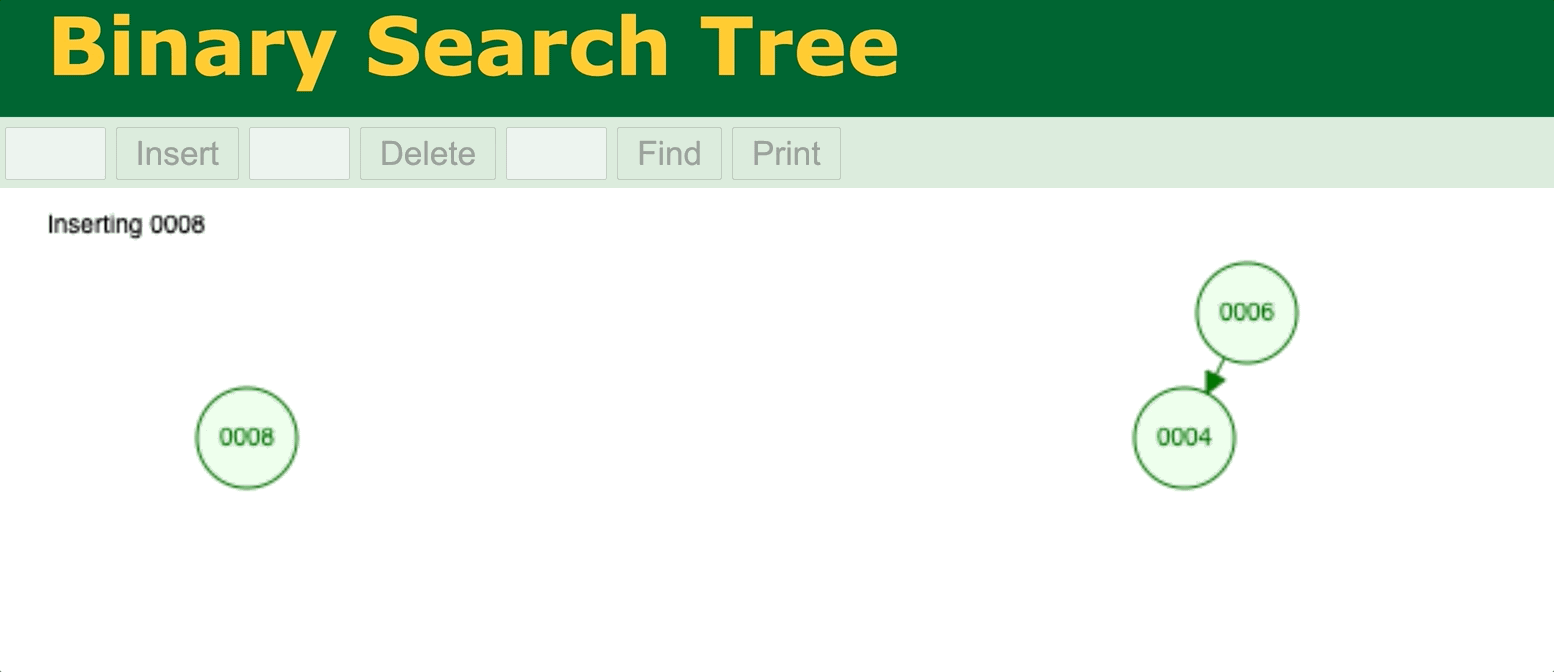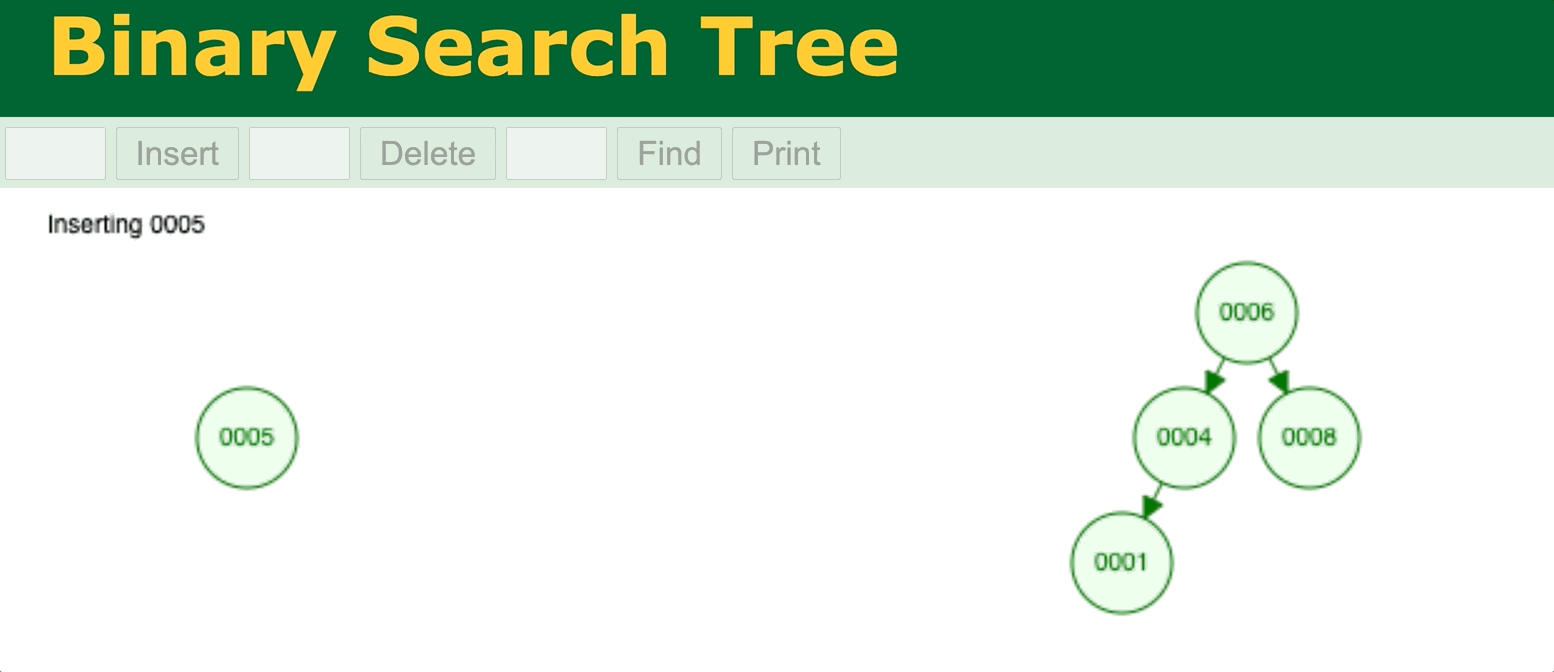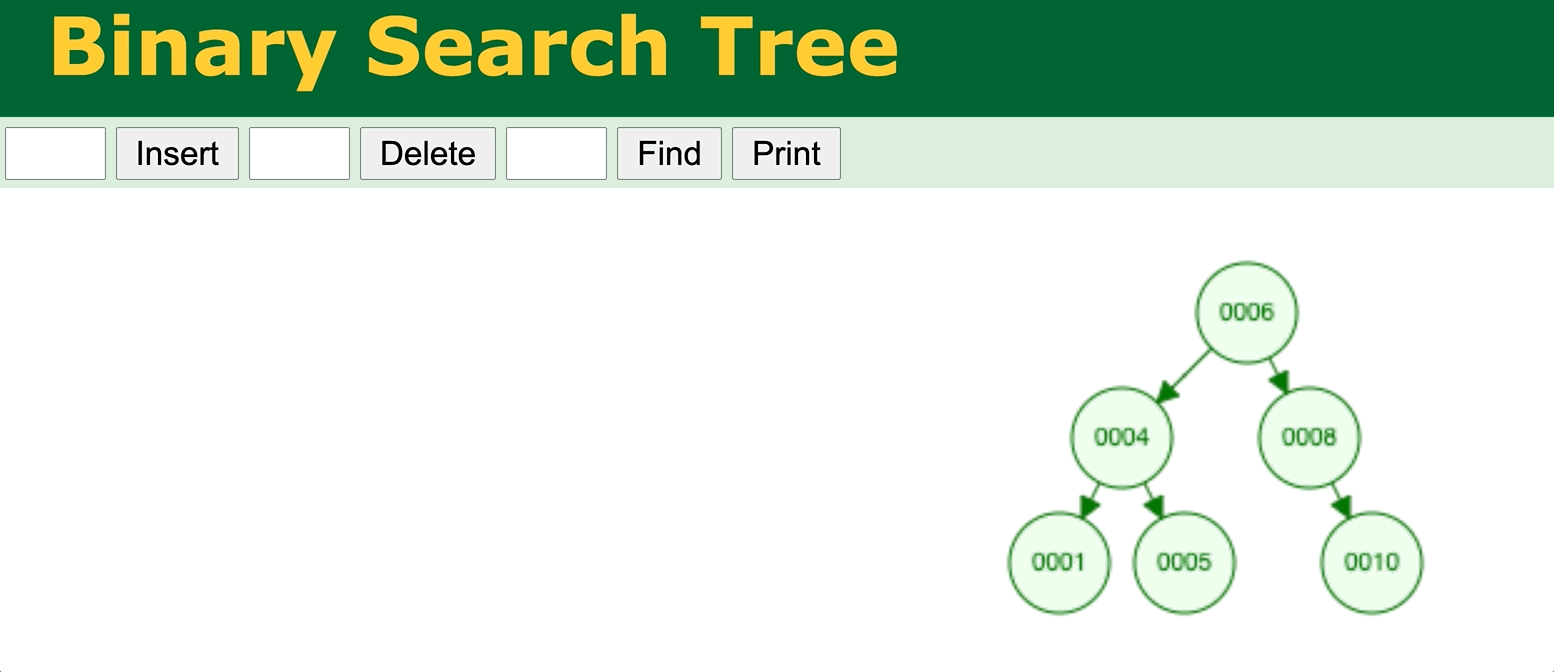
⬆️ Binary Search Tree data insertion without self-balancing 2. Try it yourself
Binary Search Tree (BST) with self-balancing mechanism
- Balanced Binary Tree: left and right subtrees of every node differ in height by no more than 1.
- Automatically run balancing method (O(logn)) after changes on
insert/delete. - Tree is always balanced.
- 2 popular BST balancing algorithms: AVL, Red-Black (AVL tree, Red-Black tree).
- Both AVL and Red-Black trees have: O(logn) on
insert/delete/searchoperation.
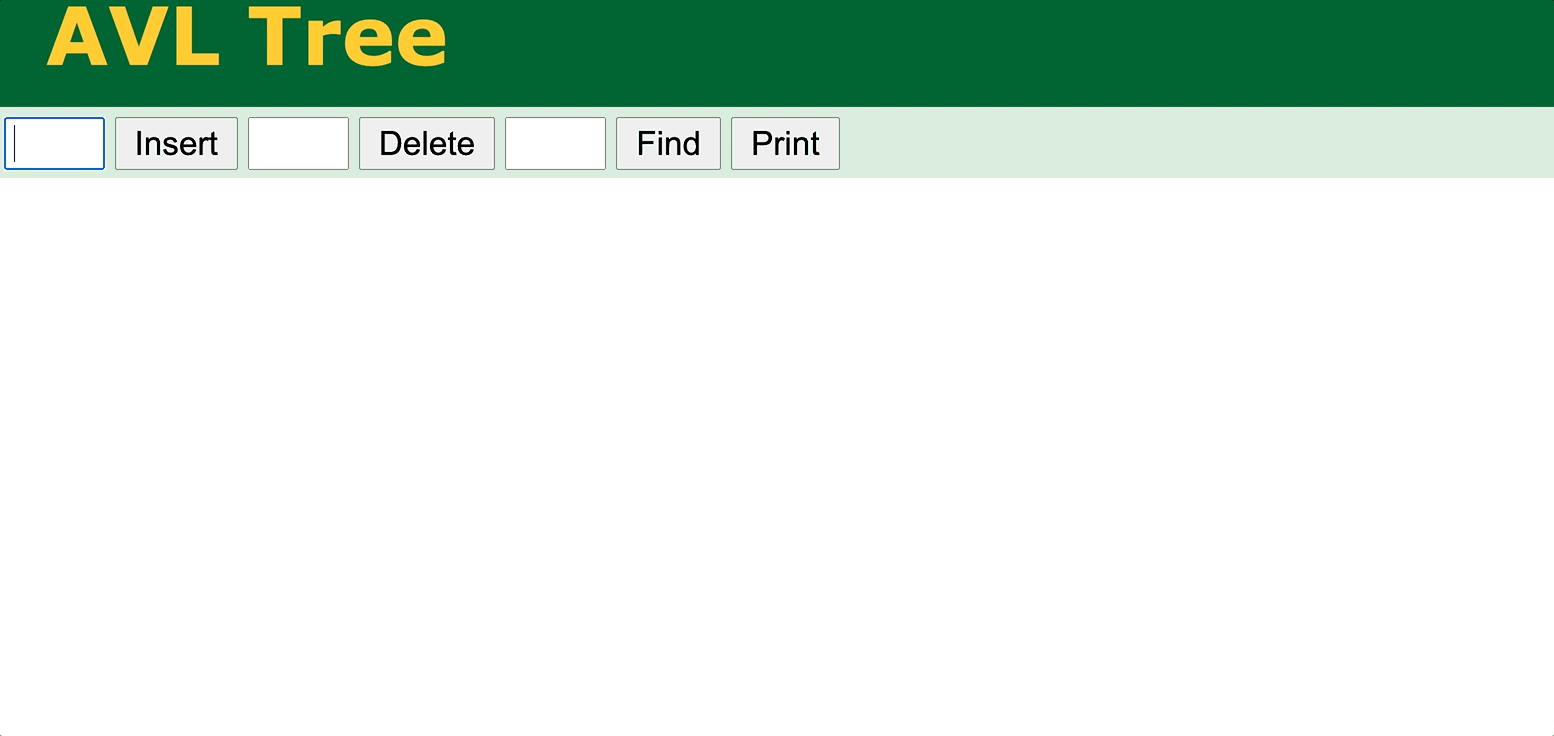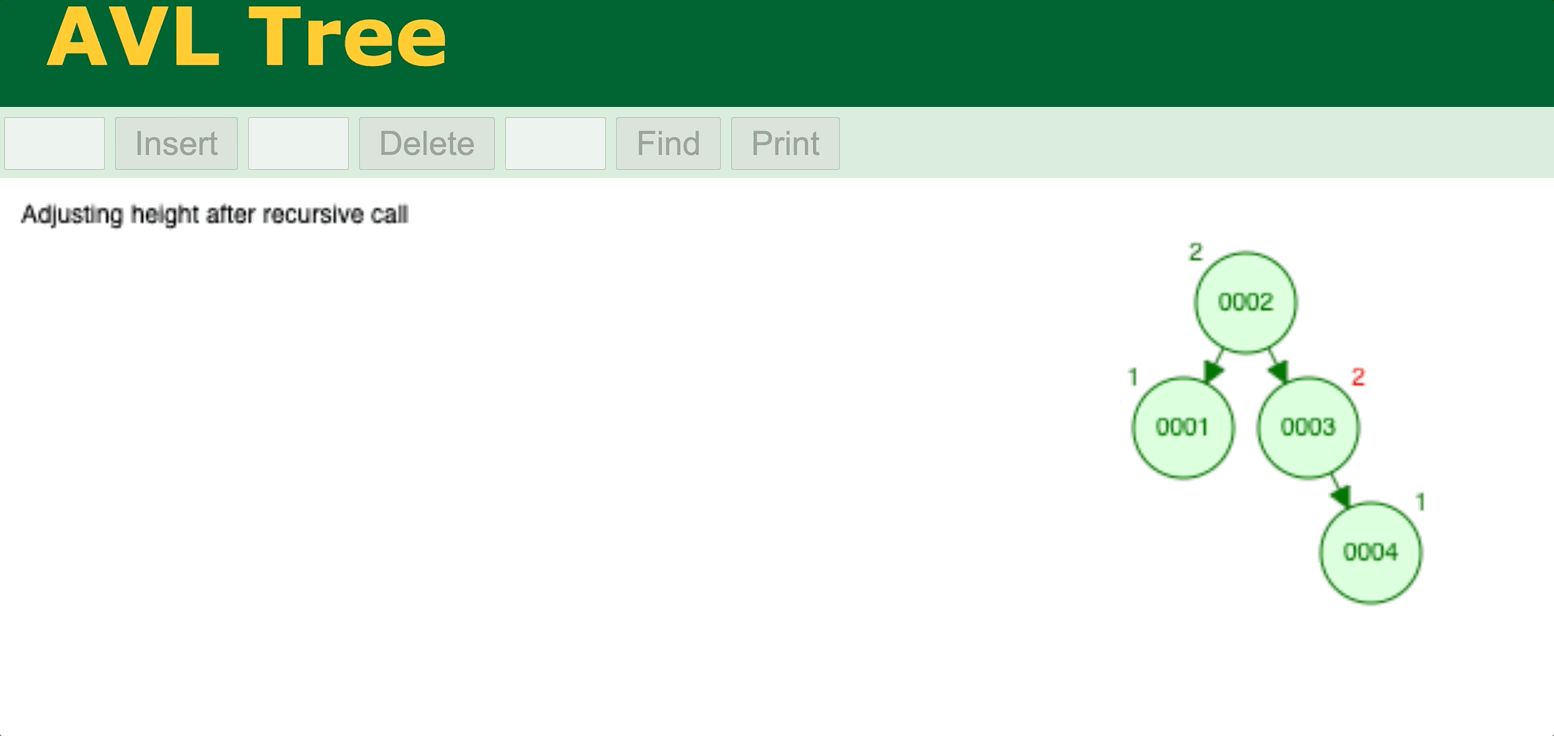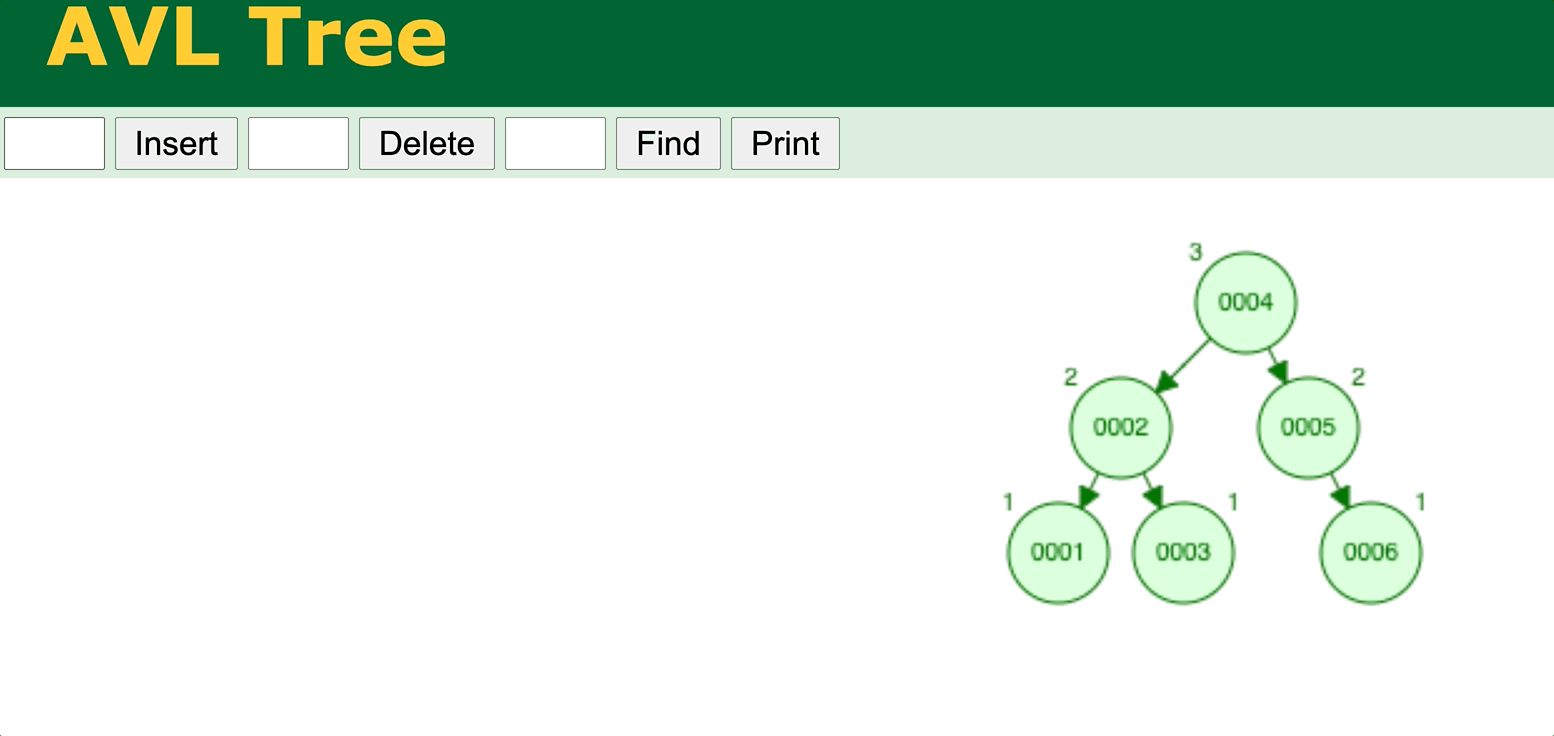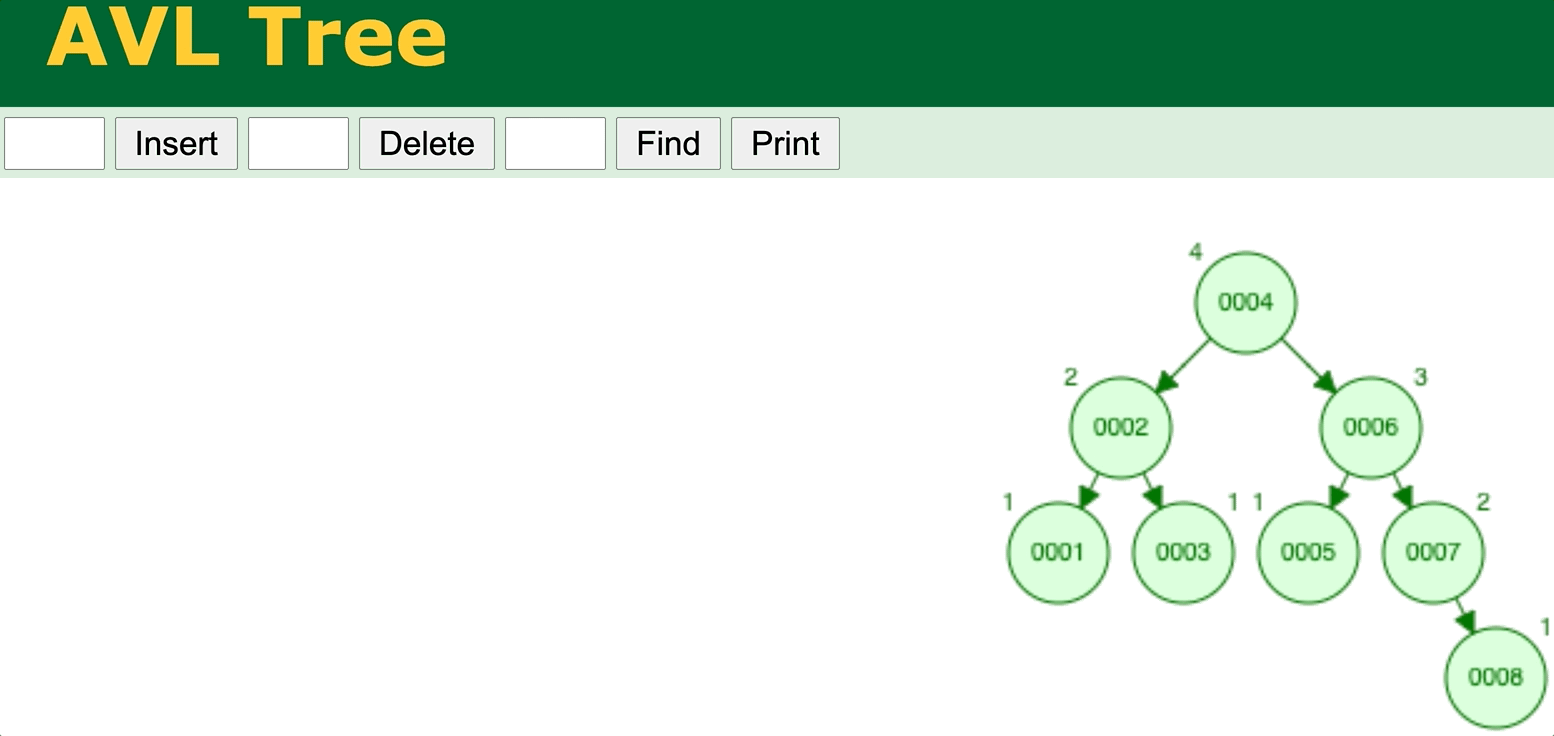
⬆️ Binary Search Tree data insertion with AVL self-balancing (AVL tree). Try it yourself
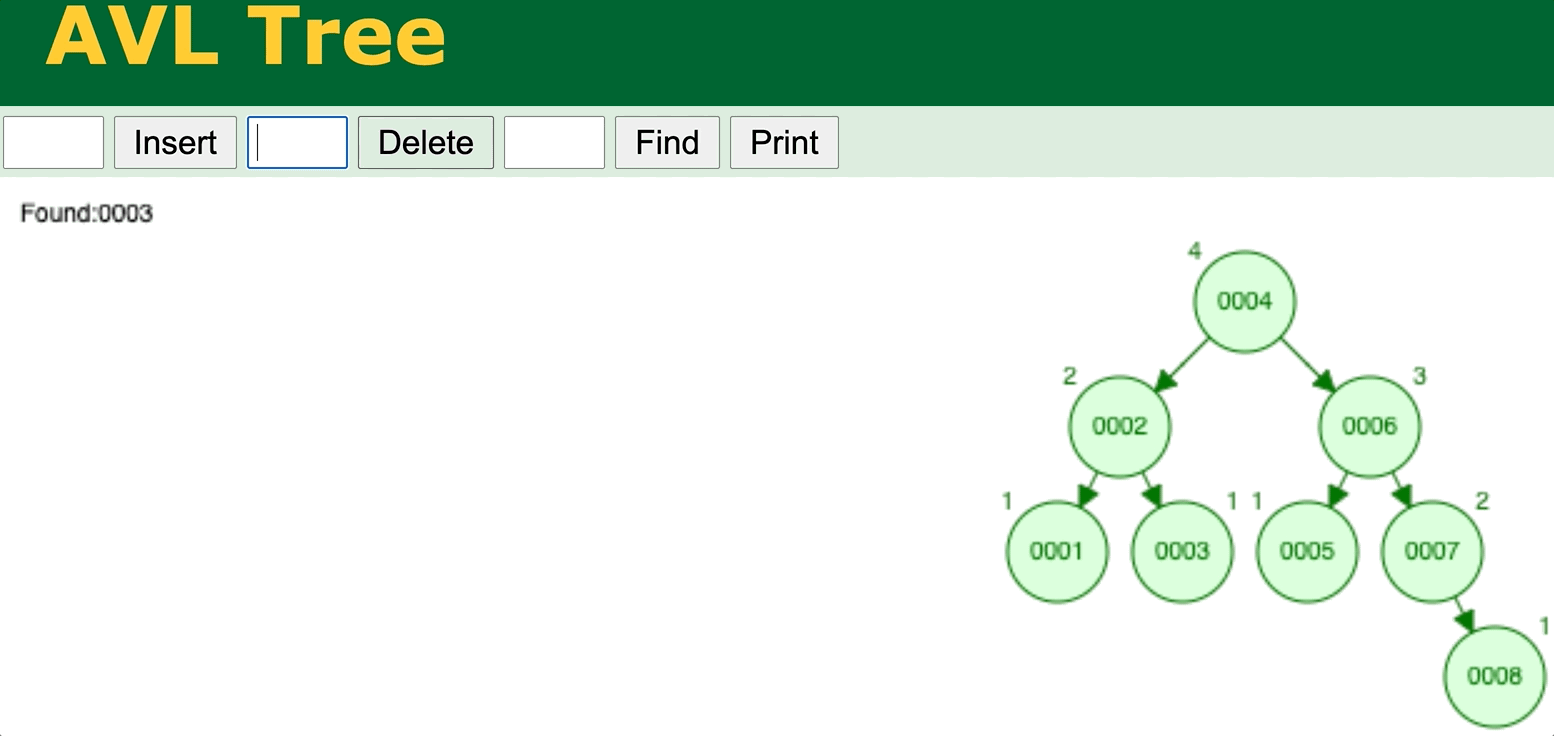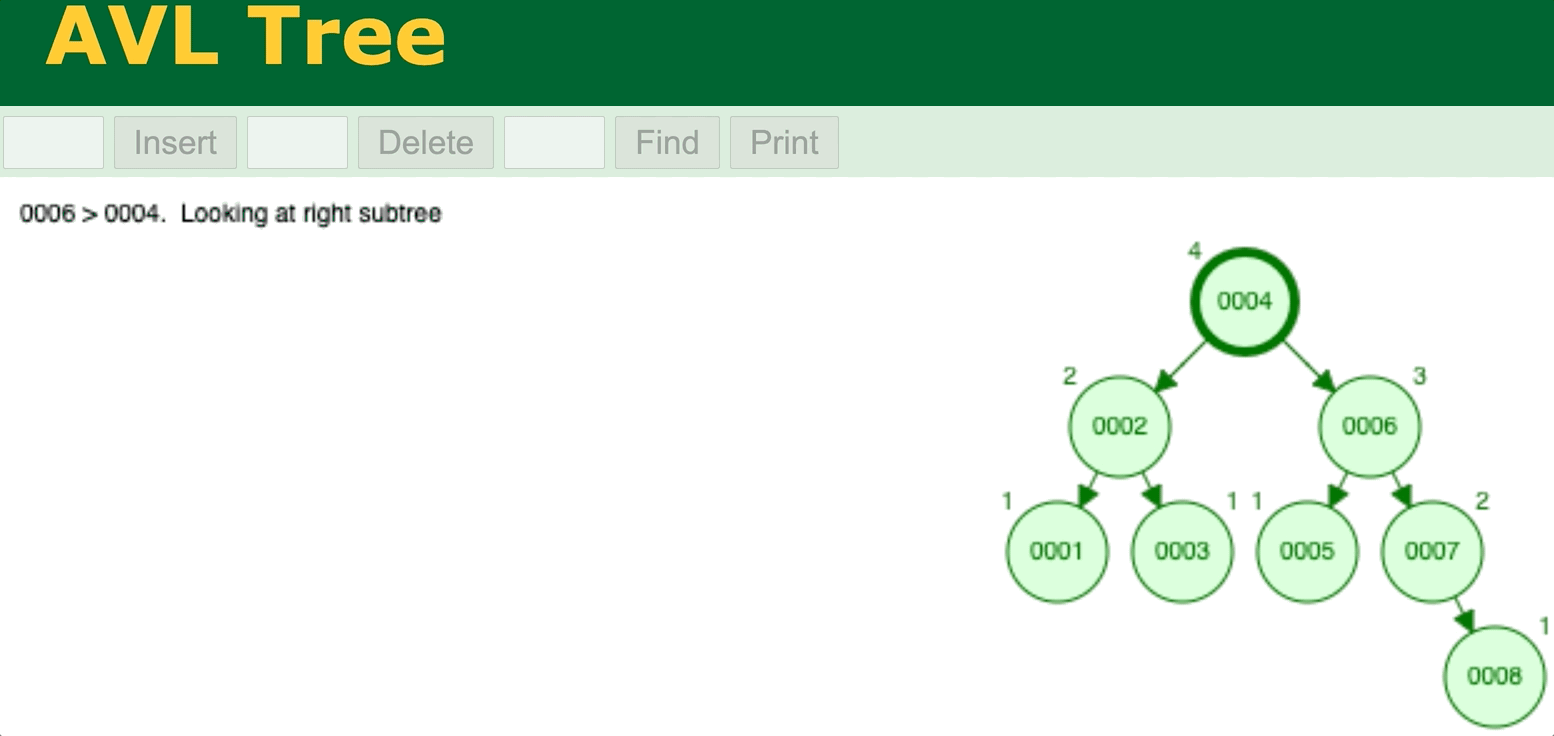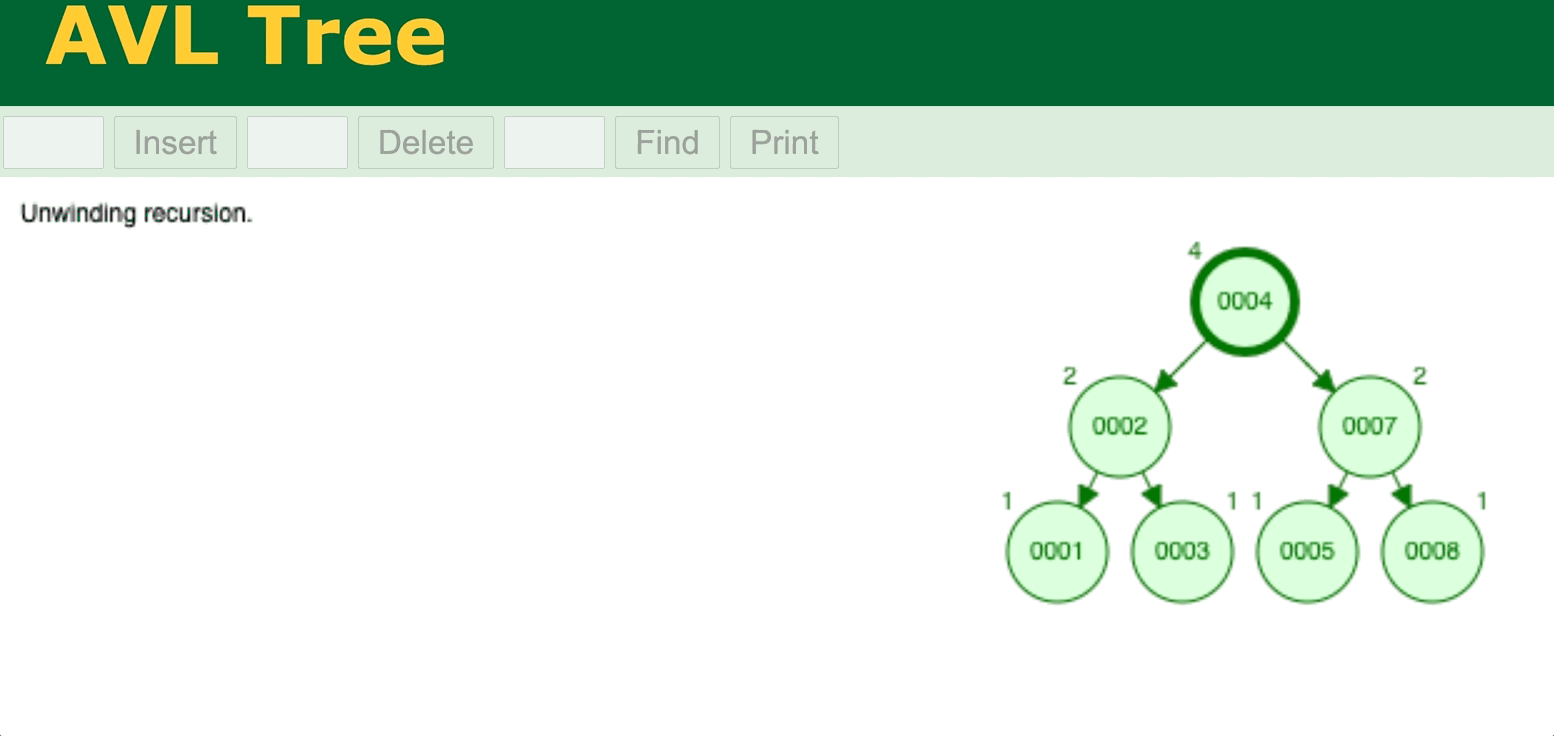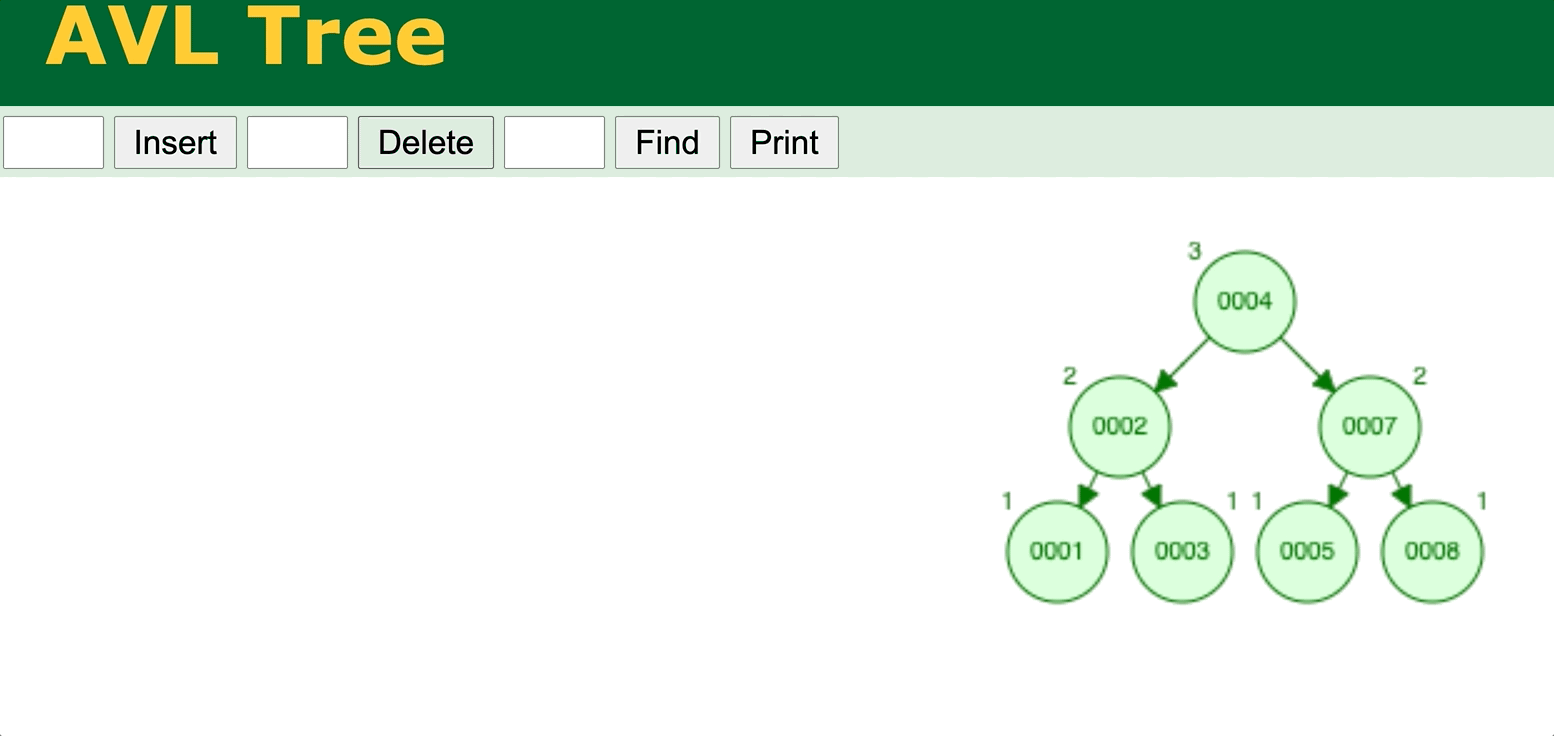
⬆️ AVL Tree delete operation. Try it yourself
Build Binary Search Tree (BST) data structure
lecture-11/binary-search-tree-data-structure.js
// structure of a node
class Node {
constructor(data) {
this.data = data
this.left = null
this.right = null
}
}
// Binary Search Tree, without self-balancing
class BinarySearchTree {
constructor(data) {
this.root = data ? new Node(data) : null
}
// insert data to tree
insert(data) {
const node = this.root
if(this.root === null) {
this.root = new Node(data)
} else {
searchLeaf(node)
function searchLeaf(node) {
if(data < node.data) {
if(node.left === null) {
return node.left = new Node(data)
}
searchLeaf(node.left)
} else if(data > node.data) {
if(node.right === null) {
node.right = new Node(data)
}
searchLeaf(node.right)
} else {
return null
}
}
}
}
// find min value in binary search tree
findMin() {
let current = this.root
while(current.left !== null) {
current = current.left
}
return current.data
}
// find max value in binary search tree
findMax() {
let current = this.root
while(current.right !== null) {
current = current.right
}
return current.data
}
// check if data is in binary search tree
exist(data) {
let current = this.root
while(current) {
if(current.data === data) {
return true
} else if(current.data > data) {
current = current.left
} else {
current = current.right
}
}
return false
}
// remove a node from binary tree
remove(data) {
this.root = removeNode(this.root, data)
function removeNode(node, data) {
// root node/tree has nothing in it
if(node == null) {
return null
}
if(data < node.data) { // move left
node.left = removeNode(node.left, data)
} else if(data > node.data) { // move to right
node.right = removeNode(node.right, data)
} else { // found matching node
if(node.left === null && node.right === null) { return null } // no children
if(node.left === null) { return node.right } // has right child
if(node.right === null) { return node.left } // has left child
let rightThenFarthestLeft = node.right; // has both left, right child
while(rightThenFarthestLeft.left !== null) {
rightThenFarthestLeft = rightThenFarthestLeft.left;
}
node.data = rightThenFarthestLeft.data;
removeNode(node.right, rightThenFarthestLeft.data);
}
return node;
}
}
// preorder traversal
preOrder() {
if (this.root == null) {
return null
} else {
var result = []
traversePreOrder(this.root)
return result
function traversePreOrder(node) {
result.push(node.data)
node.left && traversePreOrder(node.left)
node.right && traversePreOrder(node.right)
}
}
}
// inorder traversal (print min -> max)
inOrder() {
if (this.root == null) {
return null
} else {
var result = []
traverseInOrder(this.root)
return result
function traverseInOrder(node) {
node.left && traverseInOrder(node.left)
result.push(node.data)
node.right && traverseInOrder(node.right)
}
}
}
// postorder traversal
postOrder() {
if (this.root == null) {
return null
} else {
var result = []
traversePostOrder(this.root)
return result
function traversePostOrder(node) {
node.left && traversePostOrder(node.left)
node.right && traversePostOrder(node.right)
result.push(node.data)
}
}
}
printMaxToMin() {
if (this.root == null) {
return null
} else {
var result = []
traverseInOrder(this.root)
return result
function traverseInOrder(node) {
node.right && traverseInOrder(node.right)
result.push(node.data)
node.left && traverseInOrder(node.left)
}
}
}
}
const bst = new BinarySearchTree()
console.log(bst) // BinarySearchTree { root: null }
// insert data to tree
bst.insert(6)
bst.insert(4)
bst.insert(8)
bst.insert(1)
bst.insert(5)
bst.insert(10)
console.log(JSON.stringify(bst, null, 4))
// tree operations
console.log(bst.findMin()) // 1
console.log(bst.findMax()) // 10
console.log(bst.exist(100)) // false
console.log(bst.exist(8)) // true
console.log(bst.remove(8)) // undefined
console.log(JSON.stringify(bst, null, 4))
console.log(bst.exist(8)) // false
console.log(bst.inOrder()) // [ 1, 4, 5, 6, 10 ]
console.log(bst.printMaxToMin()) // [ 10, 6, 5, 4, 1 ]
console.log(bst.preOrder()) // [ 6, 4, 1, 5, 10 ]
console.log(bst.postOrder()) // [ 1, 5, 4, 10, 6 ]$ node binary-search-tree-data-structure.js
BinarySearchTree { root: null }
{
"root": {
"data": 6,
"left": {
"data": 4,
"left": {
"data": 1,
"left": null,
"right": null
},
"right": {
"data": 5,
"left": null,
"right": null
}
},
"right": {
"data": 8,
"left": null,
"right": {
"data": 10,
"left": null,
"right": null
}
}
}
}
1
10
false
true
preOrder(): [ 6, 4, 1, 5, 8, 10 ]
inOrder(): [ 1, 4, 5, 6, 8, 10 ]
printMaxToMin(): [ 10, 8, 6, 5, 4, 1 ]
postOrder(): [ 1, 5, 4, 10, 8, 6 ]