This tutorial is a part of the Data Structures and Algorithms class:
- Understanding function call stack in Javascript
- Understanding recursion
- Understanding multiple recursive calls within a function
Understanding function call stack in Javascript
Javascript function call stack is a stack:
- to keep track of the chronological order (top -> down, left -> right) which the functions are called.
- this is how computer process a function which depends on output(s) of another function(s).
- max stack size varies, depends on browser implementation. Ex: Safari 9: 63444, Chrome 51: 41753.
- if we're not careful in our program and exhaust the max stack size, it'll crash the program.
- the next function will not be executed if the current function is not done. Important note for recursion!
lecture-11/function-call-stack.js
const getStockPrice = () => 10
const getPurchasePrice = (volume) => volume * getStockPrice()
const getAvailableCash = () => 300
console.log(getAvailableCash()) // 300
console.log(getPurchasePrice(20)) // 200$ node function-call-stack.js
300
200Understanding recursion
- Formal definition:
Recursionis defined by two properties: 1. a simple base case (or cases), a terminating scenario that does not use recursion to produce an answer. 2. a recursive step, a set of rules that reduces all successive cases toward the base case. - In the call stack: all cases stack up to wait for the base case(s) output(s).
- Informal definition
Recursive function=function calls itself(usually with different input). Recursion functionprocesses data point after data point with the same logic by calling itself. This might sound strange to human intuition, but it makes perfect sense for computer.- Data passed into recursive call should gradually exhaust. Otherwise, callstack errors exceed max size.
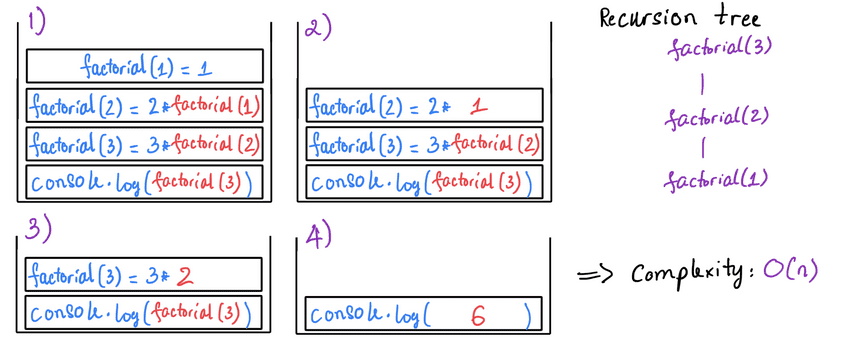
lecture-11/recursion-factorial.js
// function to return factorial (n!) of a given number `n`
const factorial = (n) => {
console.log('n:', n)
if(n === 1) return 1
return n * factorial(n - 1)
}
// 3! = 3 * 2 * 1 = 6
console.log(factorial(3)) // 6, [all cases stack up to WAIT FOR BASE CASE OUTPUT]$ node recursion-factorial.js
n: 3
n: 2
n: 1
6Understanding multiple recursive calls within a function
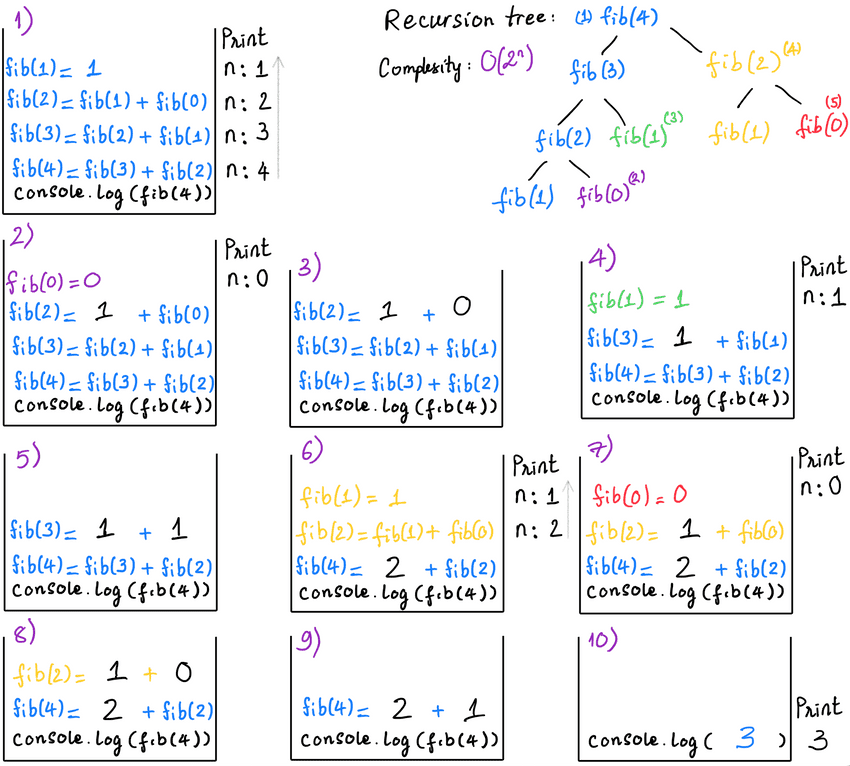
lecture-11/recursion-fibonacci.js
// function to return a Fibonacci number at a position `n`
// Fibonacci sequence: F = 0, 1, 1, 2, 3, 5, 8, 13, ...
const fib = (n) => {
console.log('n:', n)
if(n === 0) return 0
if(n === 1) return 1
return fib(n - 1) + fib(n - 2)
}
console.log(fib(4)) // 3$ node recursion-fibonacci.js
n: 4
n: 3
n: 2
n: 1
n: 0
n: 1
n: 2
n: 1
n: 0
3Real life interview questions
- Draw the call stack, recursion tree for fib function with this change:
return fib(n - 2) + fib(n - 1). What difference do you see? - Now you know about recursion, revisit Binary Search Tree data structure and build your own methods for:
insert,exist,remove,findMin,findMax.