This tutorial is a part of the Data Structures and Algorithms class:
- Problems can be solved by Dynamic Programming
- How to solve DP problems with Bellman's theory
- How to solve DP problems with MIT and the rest of the world
- How to solve DP problems with The Modern Law of Dynamic Programming (Sam's DP)
- Learn Sam's DP step 5: solve the DP problem BY HAND
- Learn Sam's DP step 6: redraw DFS state tree with code
- Learn Sam's DP step 7: calculate the information asked
- Learn Sam's DP step 8: cache distinct DFS calls
- Learn Sam's DP step 9: tips to debug a DP program
- Learn Sam's DP step 10: summary
Problems can be solved by Dynamic Programming
The Theory of Dynamic Programming - Bellman 1954 - original paper
The Theory of Dynamic Programming - Bellman 1954 - original paper with Sam's highlights


Problems can be solved by DP: finding the most optimal (value, sequence of decisons, ...) in a multi-stage decision process.
Examples of problems can be solved with DP: virtually can be found everywhere in life:
- planning of industrial production lines
- scheduling patients at a medical clinic
- determination of long term investment programs for universities
- determination of a replacement policy for machinery in factories
- programming of training policies for skilled and unskilled labor
- choice of optimal purchasing and inventory policies for department stores and military establishments
Just a simple algorithm that can be applied and make almost every single aspect of life much more optimized and better. And after learning this, it will not only highly possibly help you to get a job offer, but also help you think smarter in your daily life. Just take a moment to let this thought sink in and appreciate the beauty of this algorithm.
How to solve DP problems with Bellman's theory


How to solve DP problems with MIT and the rest of the world

⬆️ MIT 5 easy steps to solve DP

How to solve DP problems with The Modern Law of Dynamic Programming (Sam's DP)

- What we do really? We actually solve the problem by pen and paper first by following all possible choices at each state. That means we visit all possible scenarios. Visiting all sceanarios is the key importance. Because if we miss one, it's no longer guaranteed that the result is the most optimal.
- Then we leverage the knowledge we've learnt about DFS in part 1 to quickly turn our on paper solution into performant code.
Paper: The Modern Law of Dynamic Programming by Sam Tran 2023 (Sam's DP)
Paper: The Theory of Dynamic Programming - Bellman 1954 - original paper (Bellman's DP)
The Modern Law of Dynamic Programming (Sam's DP)
If you can describe your system as follow:
- A system state: is comprised of a limited number of parameters.
- Choices to change state: is a limited, known number of choices to change the system state. You have the same choices at any state.
- Final states: are the states that achieve your desired information, or the states where you can't choose any choices to change system state.
- Can reach final states: after a finite number of choices to change state, you can reach your final state(s).
- Your system can fit in a computer in terms of RAM and CPU.
Then with Sam's DP:
- You are guaranteed to have a systematic procedure to design and code your solution.
- You are guaranteed to have the best answer based on your requirements (min, max, best course of actions, ...)
- The Time and Space Complexity of your solution are always equal.
- The Time and Space Complexity will be in polynomials (One of
O(n),O(n^2), ...).- The Space Complexity equals to the number of distinct states created.
How to apply:
- We'll solve the DP problem by "running its course". Which course? All courses. With small input size (3 level DFS state tree is ideal).
- We then tell the computer how to run its course by translating the way we "run its course" by hand into code. Computers can handle much larger input sizes.
What do we do really?
- We give the computer a comprehensive way to list all possible scenarios and choose the most optimal one. That's how Sam's DP solves DP problems.
Learn Sam's DP step 5: solve the DP problem BY HAND
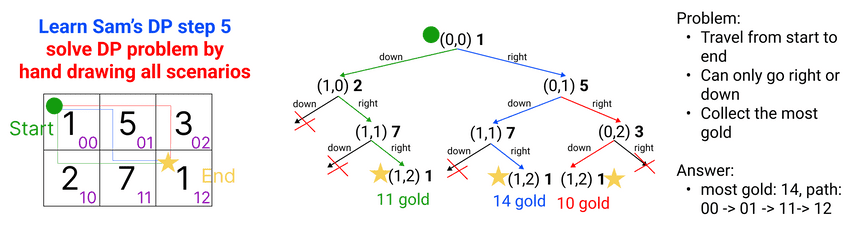
- You'll see the most difficult step is actually this step, solving the problem by hand. Some DP problems seem to be traightfoward: example: Climbing Stairs. But some are challenging, example: Edit Distance. But it is doable if you follow the steps correctly. Because all you need to do is changing system states until it reaches end state(s).
- How? List all possible scenarios with available choices. You are guaranteed to be able to do this. Because it's simply keep changing the states based on the choices the problem gives, until you can no longer have the options to change the state or you have reached your desired state(s).
- If you haven't solved it by hand, don't even think about writing a single line of code. Remember machine just repeat what it's told to do. If you can't solve it, how do you tell machine to repeat?
- Also this hand-solved problem state data is used to test if later your code is correct.
How to solve DP problem with pen and paper BY HAND - running its course:
- Choose small input size. 3 levels is ideal. Absolutely not bigger than half of an A4 tree.
- From initial state, make all possible choices to reach all possible final states.
- Once all possible scenarios are listed, choose the best scenario asked by the problem.
Learn Sam's DP step 6: redraw DFS state tree with code
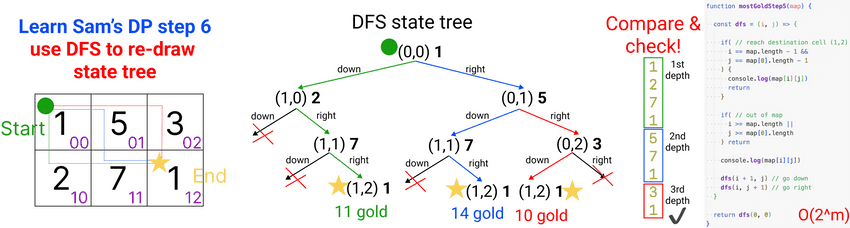
// Learn Sam's DP step 6: use DFS to recreate state tree solved by hand
// branch
function mostGoldStep5(map) {
const dfs = (i, j) => {
if( // reach destination cell (1,2)
i == map.length - 1 &&
j == map[0].length - 1
) {
console.log(map[i][j])
return
}
if( // out of map
i >= map.length ||
j >= map[0].length
) return
console.log(map[i][j])
dfs(i + 1, j) // go down
dfs(i, j + 1) // go right
}
return dfs(0, 0)
}
// time complexity: O(2^n)
// time complexity: always exponential -> very bad$ node most-gold-path.js
1
2
7
1
5
7
1
3
1
most gold: undefinedTime complexity usually in exponential: 2 choices -> 2^n, 3 choices -> 3^n, ...
REMEMBER: The number of choices at each state = the number of DFS calls.
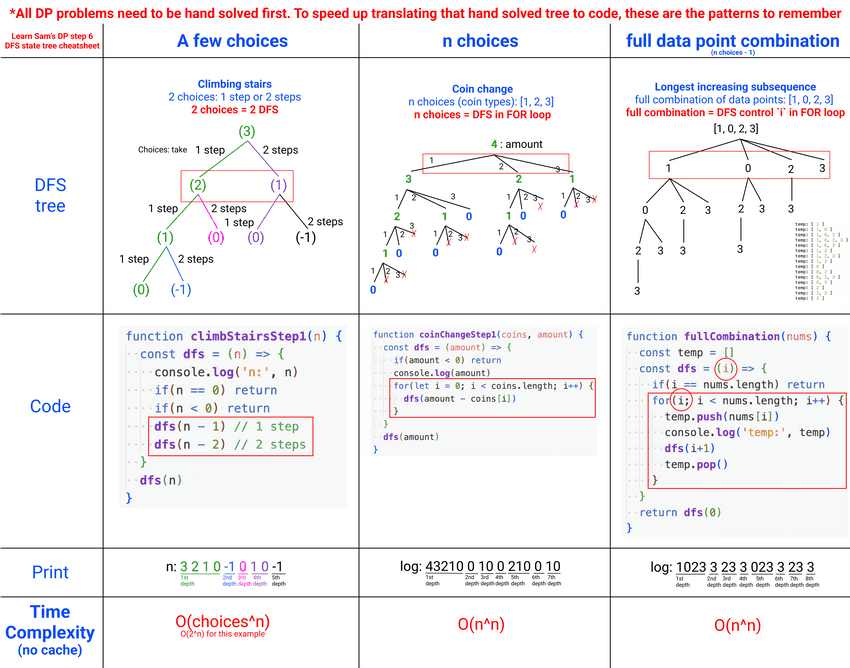
⬆️ 3 popular types of DFS State Tree generation (should learn by heart)
| Type: | a few choices |
n choices |
full data combination |
|---|---|---|---|
| Examples | Tribonacci Climbing Stairs House Robber Buy and Sell Stock Edit Distance |
Coin Change 0/1 Knapsack Dice roll with target |
Longest Increasing Subsequence Make Array Strictly Increasing Wiggle Subsequence Russian Doll Envelopes Largest Divisible Subset |
Learn Sam's DP step 7: calculate the information asked
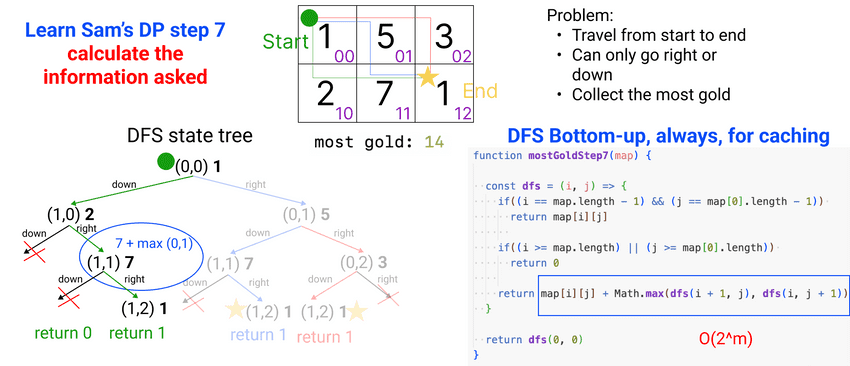
- This step should be easy as we have learnt about DFS. You can collect data top-down or bottom-up as you need.
- But for DP solution purposes, always, always, always do it bottom up. Because you can only cache with bottom-up.
// calculate
function mostGoldStep7(map) {
const dfs = (i, j) => {
if((i == map.length - 1) && (j == map[0].length - 1))
return map[i][j]
if((i >= map.length) || (j >= map[0].length))
return 0
return map[i][j] + Math.max(dfs(i + 1, j), dfs(i, j + 1))
}
return dfs(0, 0)
}$ node most-gold-path.js
most gold: 14Learn Sam's DP step 8: cache distinct DFS calls
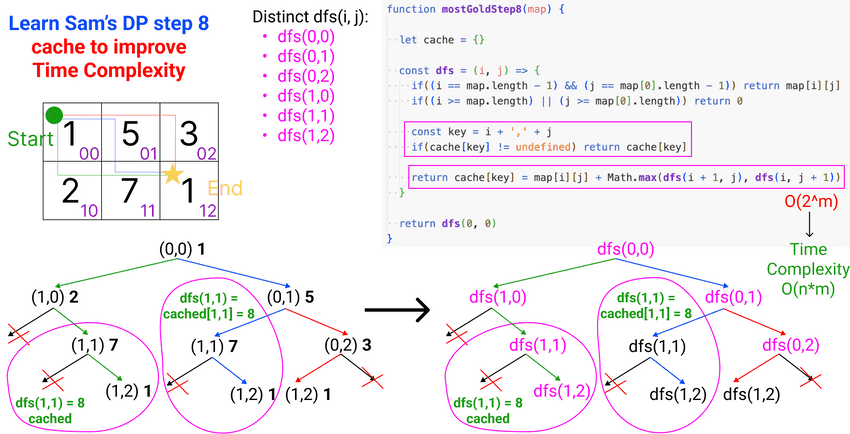
- Cache distinct DFS call = number of distinct states of the system.
- Cache space complexity = total number of distinct states of the system.
- Cache key -> all information to identify current state -> all state params combined
- Cache content: the returned value of the dfs call -> this is why we need to calculate result bottom-up.
// cache
function mostGoldStep8(map) {
let cache = {}
const dfs = (i, j) => {
if((i == map.length - 1) && (j == map[0].length - 1)) return map[i][j]
if((i >= map.length) || (j >= map[0].length)) return 0
const key = i + ',' + j
if(cache[key] != undefined) return cache[key]
return cache[key] = map[i][j] + Math.max(dfs(i + 1, j), dfs(i, j + 1))
}
return dfs(0, 0)
}$ node most-gold-path.js
most gold: 14Learn Sam's DP step 9: tips to debug a DP program
- Always compare code (states) output with hand-solved tree data.
- Place logs in every steps so you know where is the first place bug happens.
- Print trace
dfscall with its arguments. Example:dfs(1, 3, [1,2,3]) -
If you see
undefined,NaN,Infinity,-Infinityormax call stack exceedederror:- missing
base case(s) - missing
branch killing conditions undefinedvariable in calculation equation
- missing
// tips to debug a DP program
function coinChangeStep2(coins, amount) {
const dfs = (amount) => {
console.log('1111111111111')
if(amount == 0) {
console.log('2222222222222')
return 0
}
console.log('33333333333333')
const changes = []
for(let i = 0; i < coins.length; i++) {
if(amount >= coins[i]) {
console.log(`calling: dfs(${amount - coins[i]})`)
changes.push(1 + dfs(amount - coins[i]))
}
}
console.log('444444444444444')
return Math.min.apply(null, changes)
}
return dfs(amount)
}
console.log('coinChangeStep2:', coinChangeStep2([1,2,3], 4)) // 2$ node how-to-debug-dp.js
1111111111111
33333333333333
calling: dfs(3)
1111111111111
33333333333333
calling: dfs(2)
...Learn Sam's DP step 10: summary
After understanding the nature of the call stack code execution, the role of DFS, how to solve DP problem by hand, how to code the DFS state tree, how to calculate, where the first calculation is, what do we cache and how to cache, you can apply these 3 simple steps solve any DP problem:
- Step 0: check: is it/can it be a multi-stage decision process?
- Step 1: solve: the problem with pen and paper. Then use DFS to code the state tree.
- Step 2: calculate: the information asked, bottom-up.
- Step 3: cache: distinct DFS calls. Time, Space complexity = number of distinct DFS calls = total number of distinct states.
| Type: | a few choices |
n choices |
full data combination |
|---|---|---|---|
| Examples | Tribonacci Climbing Stairs House Robber Buy and Sell Stock Edit Distance |
Coin Change 0/1 Knapsack Dice roll with target |
Longest Increasing Subsequence Make Array Strictly Increasing Wiggle Subsequence Russian Doll Envelopes Largest Divisible Subset |
Real life interview questions
- What characteristics make a problem to be categorized as a Dynamic Programming problem?
- What is the idea of solving DP problems stated with The modern Law of Dynamic Programming (Sam's DP)? What's the difference between Sam's DP and Bellman's DP?
- You only need one step to solve DP by pen and paper. What is that one step?
- How to redraw DFS state tree in hand-solved DP problem with code? What are the 3 most popular patterns to do so? What is the Time Complexity of these patterns?
- Use counting method to calculate the Time Complexity of the 3 popular DFS state tree patterns.
- Try to calculate the information asked by the example above top-down, then cache it. Why should we always calculate bottom-up?
- What do we cache? And why do we need to cache DP solutions? What is the Time & Space complexity of a Sam's DP solution after caching?
- Leetcode #198. House Robber
- Leetcode #72. Edit Distance