*Prerequisite: Graph data structure.
This tutorial is a part of the Data Structures and Algorithms class:
Part 1 (05:46):
Part 2 (11:58):
- Depth First Search example 1: search with graph, TOP -> DOWN
- Depth First Search example 2: search with graph, BOTTOM -> UP
Part 3 (05:46):
- Depth First Search example 3: search with matrix
- Typical problems solved by Depth First Search algorithm
- Summary
What is Depth First Search algorithm?
- Depth First Search (DFS): visits all nodes. Only visit a node one time.
- DFS: search as deep as you can first. How deep? Can go no further deep. Then next new possible depth.
- DFS usefulness: problem that visiting nodes in depth is useful.
- Always use Stack to implement DFS algorithm.
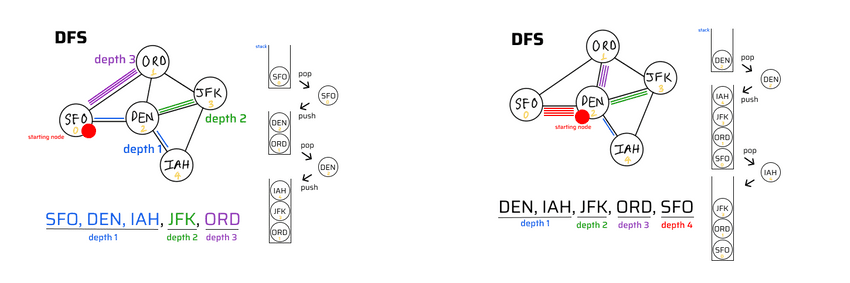
lecture-27/depth-first-search-pure.js
// Depth First Search implementation in purest form
// relationship between nodes
const graph5 = [
[1, 2], // SFO, index 0
[0, 2, 3], // ORD, index 1
[0, 1, 3, 4], // DEN, index 2
[1, 2, 4], // JFK, index 3
[2, 3], // IAH, index 4
]
// nodes' information
const idxToAirport = {
'0': { name: 'SFO' },
'1': { name: 'ORD' },
'2': { name: 'DEN' },
'3': { name: 'JFK' },
'4': { name: 'IAH' }
}
const depthFirstSearchPure = (initNodeIdx) => {
const result = []
const seen = new Set()
const stack = [initNodeIdx] // REMEMBER to use a proper stack data structure IRL
console.log('Starting airport: ', idxToAirport[initNodeIdx].name)
while(stack.length > 0) {
const curNodeIdx = stack.pop() // pop the stack
// if we've never seen this node before, process,
// otherwise, ignore the node
if(!seen.has(curNodeIdx)) {
seen.add(curNodeIdx) // add this node to seen list
const curNodeNeighbors = graph5[curNodeIdx] // get the neighbors
curNodeNeighbors.forEach(nodeIdx =>
!seen.has(nodeIdx) && stack.push(nodeIdx)) // push neighbor on top
result.push(idxToAirport[curNodeIdx].name) // save current node to result
console.log('result: ', result)
}
}
}
depthFirstSearchPure(0) // result: [ 'SFO', 'DEN', 'IAH', 'JFK', 'ORD' ]$ node depth-first-search-pure.js
Starting airport: SFO
result: [ 'SFO' ]
result: [ 'SFO', 'DEN' ]
result: [ 'SFO', 'DEN', 'IAH' ]
result: [ 'SFO', 'DEN', 'IAH', 'JFK' ]
result: [ 'SFO', 'DEN', 'IAH', 'JFK', 'ORD' ]Depth First Search example 1: search with graph, TOP -> DOWN
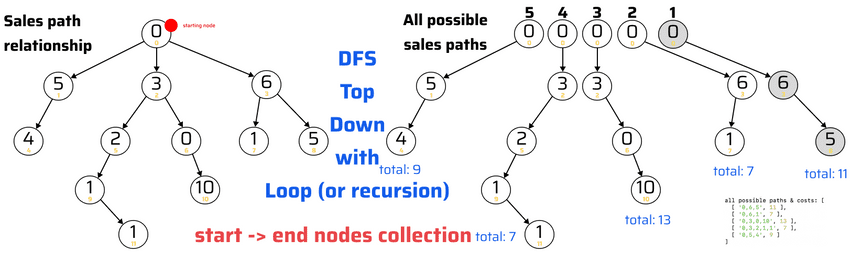
lecture-27/sales-path-with-loop.js
// Sales path DFS Loop style
// prepare path data
let nodeCount = 1
// Constructor to create a new Node
function Node(cost) {
this.cost = cost
this.children = []
this.id = nodeCount++
}
//
var root = new Node(0)
root.children.push(new Node(5))
root.children.push(new Node(3))
root.children.push(new Node(6))
root.children[0].children.push(new Node(4))
root.children[1].children.push(new Node(2))
root.children[1].children.push(new Node(0))
root.children[2].children.push(new Node(1))
root.children[2].children.push(new Node(5))
root.children[1].children[0].children.push(new Node(1))
root.children[1].children[1].children.push(new Node(10))
root.children[1].children[0].children[0].children.push(new Node(1))
// console.log(JSON.stringify(root, null, 4))
// done preparing path data
// depth first search on sales path, using WHILE LOOP
const dfsSalesPath = (node) => {
const seen = new Set()
const stack = [node] // REMEMBER to use a proper stack data structure IRL
const path = [] // current path
const paths = [] // all possible paths
while(stack.length > 0) {
printStack(stack)
const curNode = stack.pop() // pop the stack
// if we see a separator
if(curNode === '|') {
path.pop() // remove parent node from path
continue // and continue to next node
} else { // if not
path.push(curNode.cost) // save current node into path
}
// if we've never seen this node before, process,
// otherwise, ignore the node
if(!seen.has(curNode.id)) {
seen.add(curNode.id) // add this node to seen list
let seenAllChildNodes = true
let pushedSeparator = false
curNode.children.forEach(node => {
if(!seen.has(node.id)) {
if(pushedSeparator === false) {
stack.push('|')
pushedSeparator = true
}
stack.push(node) // push neighbor on top
seenAllChildNodes = false
}
})
// pop the current path when we're at a leaf node
// or all adjacent nodes have been visited
if (
curNode.children.length === 0 || // at leaf node
seenAllChildNodes // or have seen all adjacent nodes
) {
paths.push([
path.join(','),
path.reduce((partialSum, cut) => partialSum + parseInt(cut), 0)
])
path.pop()
}
// console.log("path:", path)
}
}
return paths
}
console.log('all possible paths & costs:', dfsSalesPath(root))
// print node `cost` instead of the whole node object
function printStack (stack) {
const print = []
for(let el of stack) {
if(el === '|') {
print.push(el)
} else {
print.push(el.cost)
}
}
console.log('stack:', print)
}$ node sales-path-with-loop.js
stack: [ 0 ]
stack: [ '|', 5, 3, 6 ]
stack: [ '|', 5, 3, '|', 1, 5 ]
stack: [ '|', 5, 3, '|', 1 ]
stack: [ '|', 5, 3, '|' ]
stack: [ '|', 5, 3 ]
stack: [ '|', 5, '|', 2, 0 ]
stack: [ '|', 5, '|', 2, '|', 10 ]
stack: [ '|', 5, '|', 2, '|' ]
stack: [ '|', 5, '|', 2 ]
stack: [ '|', 5, '|', '|', 1 ]
stack: [ '|', 5, '|', '|', '|', 1 ]
stack: [ '|', 5, '|', '|', '|' ]
stack: [ '|', 5, '|', '|' ]
stack: [ '|', 5, '|' ]
stack: [ '|', 5 ]
stack: [ '|', '|', 4 ]
stack: [ '|', '|' ]
stack: [ '|' ]
all possible paths & costs: [
[ '0,6,5', 11 ],
[ '0,6,1', 7 ],
[ '0,3,0,10', 13 ],
[ '0,3,2,1,1', 7 ],
[ '0,5,4', 9 ]
]Depth First Search example 2: search with graph, BOTTOM -> UP
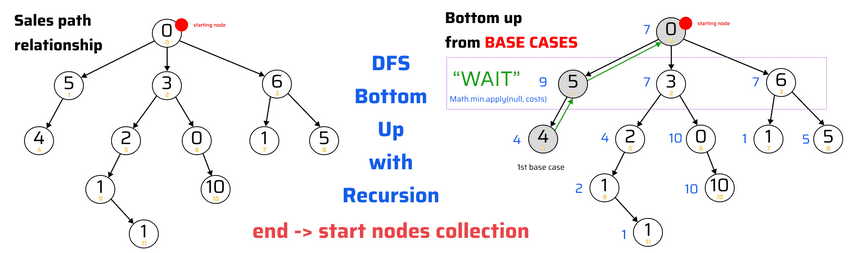
lecture-27/sales-path-bottom-up-recursion.js
// Sales path DFS recursion style
// prepare path data
let nodeCount = 1
// Constructor to create a new Node
function Node(cost) {
this.cost = cost
this.children = []
this.id = nodeCount++
}
//
var root = new Node(0)
root.children.push(new Node(5))
root.children.push(new Node(3))
root.children.push(new Node(6))
root.children[0].children.push(new Node(4))
root.children[1].children.push(new Node(2))
root.children[1].children.push(new Node(0))
root.children[2].children.push(new Node(1))
root.children[2].children.push(new Node(5))
root.children[1].children[0].children.push(new Node(1))
root.children[1].children[1].children.push(new Node(10))
root.children[1].children[0].children[0].children.push(new Node(1))
// console.log(JSON.stringify(root, null, 4))
// done preparing path data
// depth first search on sales path, recursion style
const dfsSalesPathRecursion = (rootNode) => {
return cost(rootNode)
function cost(node) {
if(node.children.length == 0) { // base case, aka exit condition
console.log('leaf cost:', node.cost)
return node.cost
} else {
let costs = new Array(node.children.length)
for(let i = 0; i < node.children.length; i++) {
costs[i] = node.cost + cost(node.children[i])
}
console.log('min from costs:', costs)
return Math.min.apply(null, costs)
}
}
}
console.log('cheapest path cost:', dfsSalesPathRecursion(root)) // 7$ node sales-path-bottom-up-recursion.js
leaf cost: 4
min from costs: [ 9 ]
leaf cost: 1
min from costs: [ 2 ]
min from costs: [ 4 ]
leaf cost: 10
min from costs: [ 10 ]
min from costs: [ 7, 13 ]
leaf cost: 1
leaf cost: 5
min from costs: [ 7, 11 ]
min from costs: [ 9, 7, 7 ]
cheapest path cost: 7Depth First Search example 3: search with matrix
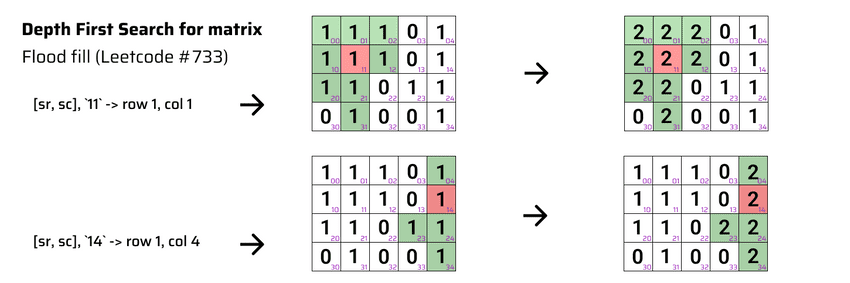
lecture-26/shortest-path-matrix.js
// Leetcode #733 Flood fill: https://leetcode.com/problems/flood-fill/description/
// DFS flood fill
var floodFill = function(image, sr, sc, color) {
console.log('image:', image)
const stack = [[sr, sc]] // REMEMBER to use a proper stack data structure IRL
const seen = new Set()
while(stack.length > 0) {
// console.log(stack)
const [curSr, curSc] = stack.pop() // pop the stack
const curPosStr = '' + curSr + curSc
// if we never seen this node before, process
if(!seen.has(curPosStr)) {
seen.add(curPosStr)
const floodVal = image[curSr][curSc] // get starting pixel value
image[curSr][curSc] = color // update starting pixel to `color`
const neighbors = [ // list of all possible neighbors
[curSr + 1, curSc],
[curSr - 1, curSc],
[curSr, curSc + 1],
[curSr, curSc - 1],
]
for(let [nSr, nSc] of neighbors) { // for each neighbor
const nPosStr = '' + nSr + nSc
if(
!seen.has(nPosStr) && // never seen
nSr >= 0 && nSr < image.length && // within image width
nSc >= 0 && nSc < image[0].length && // within image height
image[nSr][nSc] == floodVal // same pixel value with started pixel
) {
stack.push([nSr, nSc]) // push node on top the stack
}
}
}
} // otherwise, ignore
return image
}
const image = [
[1, 1, 1, 0, 1],
[1, 1, 1, 0, 1],
[1, 1, 0, 1, 1],
[1, 1, 0, 0, 1],
]
const sr = 1
const sc = 1
const color = 2
console.log('flood filled image:', floodFill(image, sr, sc, color))$ node flood-fill.js
image: [
[ 1, 1, 1, 0, 1 ],
[ 1, 1, 1, 0, 1 ],
[ 1, 1, 0, 1, 1 ],
[ 1, 1, 0, 0, 1 ]
]
flood filled image: [
[ 2, 2, 2, 0, 1 ],
[ 2, 2, 2, 0, 1 ],
[ 2, 2, 0, 1, 1 ],
[ 2, 2, 0, 0, 1 ]
]Typical problems solved by Depth First Search algorithm
Identify the nodes, construct the graph, apply node discovery pattern.
| Problem | BFS | DFS |
|---|---|---|
| Node visitation pattern | breadth first (layers)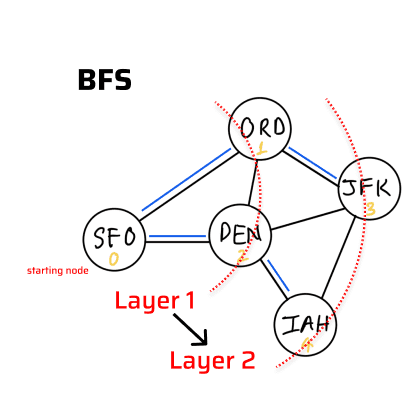
|
depth first (start <-> end)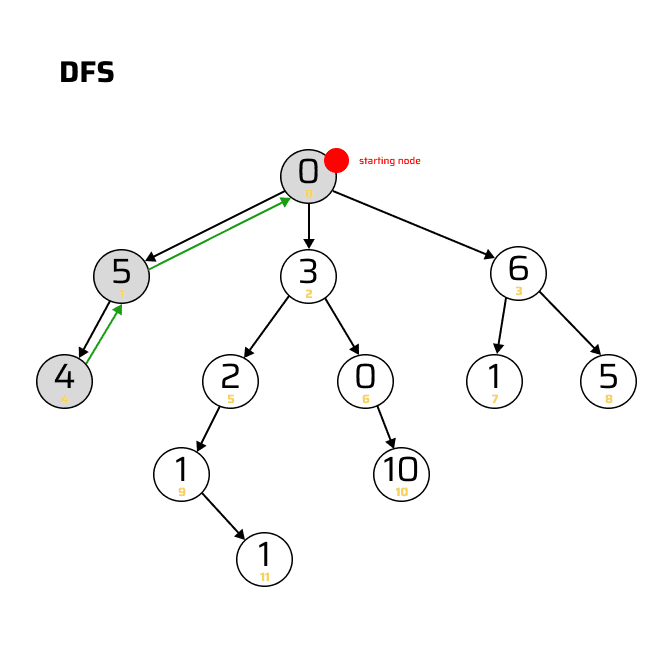
|
| Visit all nodes, each once | ✅ | ✅ |
| Shortest path (equal edges) | ✅ | ❌ |
| Shortest path (UN-equal edges) (use Bellman-Ford) |
❌ | ❌ |
| Think Top -> Down | ✅ | ✅ |
| Think Bottom -> Up | ❌ | ✅ |
| Cycle detection | ✅ | ✅ |
| Is a graph bipartite | ✅ | ✅ |
Summary
| Prob. class | P. sub-class | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|---|
| (almost) ANY problem class | array, matrix, ... | Brute Force | O(n) & up |
|
| Can try with any problem type | - pass split test - array, string or graph, ... - divide, solve, combine gives a possible solution |
Divide and Conquer | O(nlogn) |
|
- accessing 2 data points at a time is useful- closing in the pointers proven to give a correct answer - usually array or string |
Two Pointers | O(n) |
||
| 1. Maximization 2. Minimization |
array, string or graph, ... | Greedy choice, no guarantee for most optimal solution |
varies |
|
| 3. Find all options | array, matrix, ... | Brute Force | O(n) & up |
|
| 4. Find most optimal solution | ||||
| 5. Find a truth | search for a number | - sorted array or balanced BST |
Binary Search | O(logn) |
| accessing a few consecutive data points at the same time is necessary/useful | - usually array or string | Slding Window | O(n) |
|
| - shortest path, equal edge weight - node visitation layer by layer |
- graph or matrix | Breadth First Search | O(n) |
|
| - think top down, think bottom up - node visitation go full depth first |
- graph or matrix | Depth First Search | O(n) |
|
Real life interview questions
- How does Depth First Search solve problems?
- What kind of problems can typically be solved by Depth First Search?
- Recalculate the Complexity of the problems above.
- Redo the problems above. You should be able to quickly explain how the algorithm works and implement each of them within 15 mins.
- Redo example 1 and 3 with recursion.
- Draw the calltack and explain how DFS bottom-up code works in example 2.
- What are the differences of node visiting & collection between DFS Top-Down and Bottom-Up? Why are there such differences? What kind of problems can we solve with such patterns.
- (Medium) Leetcode #2368. Reachable Nodes With Restrictions
- (Medium) Leetcode #841. Keys and Rooms
- (Easy) Leetcode #1971. Find if Path Exists in Graph
- (Medium) Leetcode #1466. Reorder Routes to Make All Paths Lead to the City Zero
- (Medium) Leetcode #797. All Paths From Source to Target
- (Medium) Leetcode #207. Course Schedule
- More on Leetcode #depth-first-search.
