*Prerequisite: Graph data structure.
This tutorial is a part of the Data Structures and Algorithms class:
Part 1 (09:37):
- What is Breadth First Search algorithm?
- Breadth First Search simplest code implementation
- Typical problems solved by Breadth First Search algorithm
Part 2 (08:01):
Part 3 (10:59):
- Breadth First Search example 2: search with matrix
- How to think and solve problems with Breadth First Search
- Summary
What is Breadth First Search algorithm?
- A graph: holds the relationship between the nodes. (ex: relationship between airports, ...)
- A node: holds data that describe something in real life. (ex: airport area, number of docks, ...)
- Purpose of a graph algorithm: is to visit the nodes in a particular pattern, useful way.
- Breadth First Search: search as broad as you can first. Then level by level.
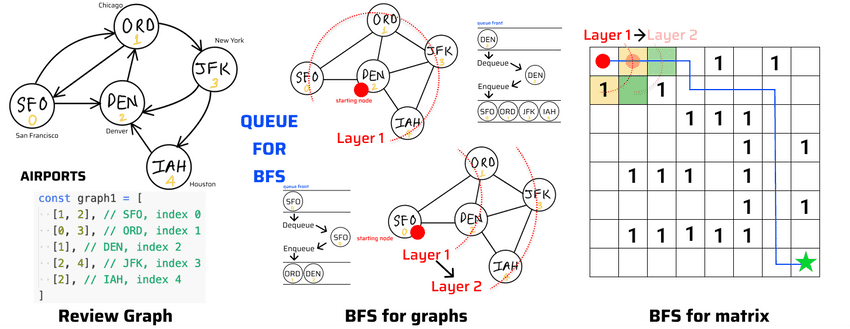
Breadth First Search simplest code implementation
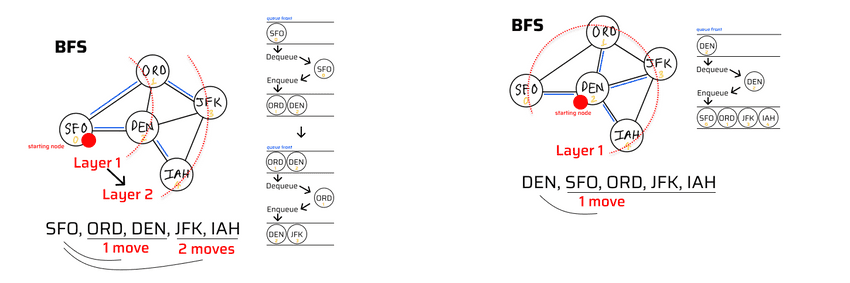
- Breadth First Search (BFS): is a graph algorithm. Pattern of node visitation: level by level (onion).
- BFS: visit all neighbor nodes before moving on to the next set of nodes. level by level (onion layers). Level 1: 1 move, level 2: 2 moves, level 3: 3 moves, ...
- BFS usefulness: shortest path (equal edge), problem that visiting nodes layer after layer is useful.
- Always use Queue to implement BFS algorithm.
lecture-26/breadth-first-search-pure.js
// Breadth First Search implementation in purest form
// relationship between nodes
const graph5 = [
[1, 2], // SFO, index 0
[0, 2, 3], // ORD, index 1
[0, 1, 3, 4], // DEN, index 2
[1, 2, 4], // JFK, index 3
[2, 3], // IAH, index 4
]
// nodes' information
const idxToAirport = {
'0': { name: 'SFO' },
'1': { name: 'ORD' },
'2': { name: 'DEN' },
'3': { name: 'JFK' },
'4': { name: 'IAH' }
}
const breadthFirstSearchPure = (initNodeIdx) => {
const result = []
const seen = new Set()
const queue = [initNodeIdx] // REMEMBER to use a proper queue data structure IRL
console.log('Starting airport: ', idxToAirport[initNodeIdx].name)
while(queue.length > 0) {
const curNodeIdx = queue.shift() // dequeue
// if we've never seen this node before, process,
// otherwise, ignore the node
if(!seen.has(curNodeIdx)) {
seen.add(curNodeIdx) // add this node to seen list
const curNodeNeighbors = graph5[curNodeIdx] // get the neighbors
curNodeNeighbors.forEach(nodeIdx =>
!seen.has(nodeIdx) && queue.push(nodeIdx)) // enqueue neighbors
result.push(idxToAirport[curNodeIdx].name) // save current node to result
console.log('result: ', result)
}
}
}
breadthFirstSearchPure(0) // result: [ 'SFO', 'ORD', 'DEN', 'JFK', 'IAH' ]$ node breadth-first-search-pure.js
Starting airport: SFO
result: [ 'SFO' ]
result: [ 'SFO', 'ORD' ]
result: [ 'SFO', 'ORD', 'DEN' ]
result: [ 'SFO', 'ORD', 'DEN', 'JFK' ]
result: [ 'SFO', 'ORD', 'DEN', 'JFK', 'IAH' ]Typical problems solved by Breadth First Search algorithm
Identify the nodes, construction the graph, apply BFS node discovery pattern (level by level) to see if it solve your problem:
- Shortest path from point A to point B (ONLY if edges weight are equal -> BFS).
- Shortest path from point A to point B (if edges weight are NOT equal -> Bellman-Ford).
- Path finding: is there a possible path between two nodes? (BFS + DFS)
- Find common friends in social network.
- Network router: best package routing.
- Web crawler strategy.
- Graph intensive: cycle detection, is a graph bipartite, ...
Breadth First Search example 1: search with graph
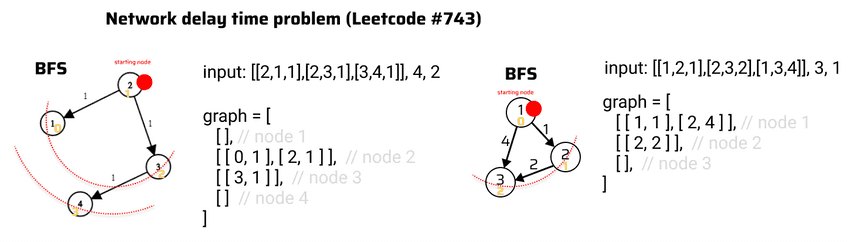
lecture-26/network-delay-time.js
// network delay time: https://leetcode.com/problems/network-delay-time/
var networkDelayTime = function(times, n, k) {
// initialize graph with empty arrays
const graph = []
for(let i = 0; i < n; i++) { graph.push([]) }
console.log('graph:', graph)
// build adjacency list graph with `times` data
for(let i = 0; i < times.length; i++) {
const nodeIdx = times[i][0] - 1
const neighborIdx = times[i][1] - 1
const travelTime = times[i][2]
graph[nodeIdx].push([neighborIdx, travelTime])
}
console.log('graph:', graph)
const initNodeIdx = k - 1 // our graph is 0-indexed from given 1-indexed data
const layerEnd = '|' // layer separator in the queue
const queue = [initNodeIdx, layerEnd] // initialize the queue
const seen = new Set([initNodeIdx]) // keep track of seen nodes
let paths = [[0, initNodeIdx]] // the first num (0) is total travel time
while(queue.length > 0) {
// console.log('queue: ', queue)
const curNodeIdx = queue.shift() // dequeue
// add layer separator `|` whenever a layer finishes
if(curNodeIdx === layerEnd && queue.length > 0) {
queue.push(layerEnd)
continue
}
// break out of the loop when there's no data left in the queue
if(curNodeIdx === layerEnd && queue.length === 0) {
break
}
const curNode = graph[curNodeIdx] // get current node neighbors
const tempPaths = [] // update paths
// for every neighbor
for(let i = 0; i < curNode.length; i++) {
const [neighborNodeIdx, neighborTravelTime] = curNode[i]
// if this neighbor hasn't been seen
if(!seen.has(neighborNodeIdx)) {
seen.add(neighborNodeIdx) // add to seen list
queue.push(neighborNodeIdx) // add to the queue
// update path with this new neighor + travel time to this neighbor
for(let j = 0; j < paths.length; j++) {
if (paths[j][paths[j].length - 1] === curNodeIdx) {
const updatePath = paths[j].concat(neighborNodeIdx)
updatePath[0] += neighborTravelTime
tempPaths.push(updatePath)
} else {
tempPaths.push(paths[j])
}
}
}
}
tempPaths.length !== 0 && (paths = tempPaths)
console.log('paths: ', paths)
}
// if we don't see all the nodes -> can't reach to every node -> return -1
if(seen.size !== n) {
return -1
} else {
let max = 0
for(let i = 0; i < paths.length; i++) {
if(paths[i][0] > max) max = paths[i][0]
}
return max
}
}
console.log(networkDelayTime([[2,1,1],[2,3,1],[3,4,1]], 4, 2)) // 2
// console.log(networkDelayTime([[1,2,1],[2,3,2],[1,3,4]],3,1)) // 4$ node network-delay-time.js
graph: [ [], [], [], [] ]
graph: [ [], [ [ 0, 1 ], [ 2, 1 ] ], [ [ 3, 1 ] ], [] ]
paths: [ [ 1, 1, 0 ], [ 1, 1, 2 ] ]
paths: [ [ 1, 1, 0 ], [ 1, 1, 2 ] ]
paths: [ [ 1, 1, 0 ], [ 2, 1, 2, 3 ] ]
paths: [ [ 1, 1, 0 ], [ 2, 1, 2, 3 ] ]
2Breadth First Search example 2: search with matrix
- The first path that reaches
77is the shortest path. Why? because it takes the same number of moves (equal edges) for any other paths.
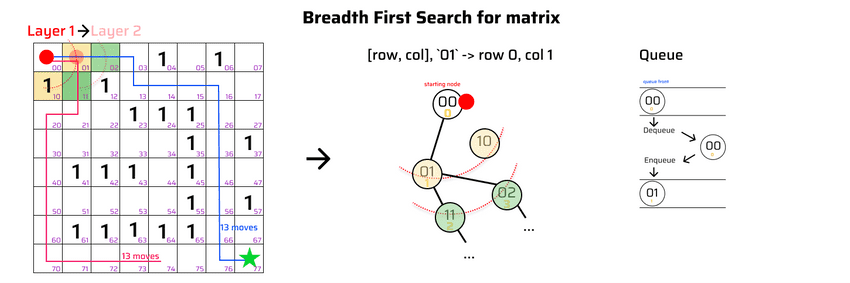
lecture-26/shortest-path-matrix.js
// BFS shortest path on matrix
const shortestPath = (map, start, end) => {
matprint(map)
console.log('starting position:', start)
console.log('target position:', end)
const queue = [start]
const seen = new Set()
let paths = [['' + start[0] + start[1]]] // initial start at `00`, [['00']]
while(queue.length > 0) {
console.log('queue:', queue)
// console.log('paths:', paths)
const [row, col] = queue.shift() // dequeue
console.log('current node (row, col):', row, col)
const strRowCol = '' + row + col // `00` etc.
if(!seen.has(strRowCol)) { // if we've never seen this node before, process
seen.add(strRowCol) // mark this node as seen
const tempPaths = [] // path + new neighbor node will be temp saved here
const seenNoNewNeiboPaths = new Set() // keep track of path has no new neighbor
// list of 4 neighbors' indexes: left, right, up, down
const neighborIdxes = [[row+1, col], [row-1, col], [row, col+1], [row, col-1]]
// for each neighbor
for(let i = 0; i < neighborIdxes.length; i++) {
const [neighborRow, neighborCol] = neighborIdxes[i]
const strNeighborRowCol = '' + neighborRow + neighborCol // `01` etc.
if(
(neighborRow < 8) && // if neighbor index is not out of
(neighborRow > -1) && // matrix (0 <= index <= 7)
(neighborCol < 8) &&
(neighborCol > -1) &&
map[neighborRow][neighborCol] !== 1 && // and movable to this neighbor
!seen.has(strNeighborRowCol) // and we've never seen that neighbor before
) {
queue.push([neighborRow, neighborCol]) // enqueue neighbor node
// update path with this neighor. AKA paths [[00]] -> paths [[00, 01]]
for(let j = 0; j < paths.length; j++) {
if (paths[j][paths[j].length - 1] === strRowCol) { // continue path
const updatePath = paths[j].concat(strNeighborRowCol)
tempPaths.push(updatePath)
if(strNeighborRowCol === '77') { // first path reaches target
matprint(map, updatePath)
return updatePath // return this path and exit
}
} else { // only save to temp path once, path with no new neighbor
!seenNoNewNeiboPaths.has(paths[j][paths[j].length - 1]) &&
tempPaths.push(paths[j])
seenNoNewNeiboPaths.add(paths[j][paths[j].length - 1])
}
}
}
}
// update paths with tempPaths
tempPaths.length !== 0 && (paths = tempPaths)
}
console.log('======================= new queue item ====')
}
// console.log('paths: ', paths)
// for(let i = 0; i < paths.length; i++) {
// matprint(map, paths[i])
// console.log('=====================================')
// }
}
const map = [
[0, 0, 0, 0, 1, 0, 1, 0],
[1, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 1],
[0, 1, 1, 1, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 1],
[0, 1, 1, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
]
console.log(shortestPath(map, [0,0], [7,7]))
/**
* Pretty print a matrix helper function
* https://gist.github.com/lbn/3d6963731261f76330af
* @param {*} mat
*/
function matprint(mat, path = []) {
let shape = [mat.length, mat[0].length];
function col(mat, i) {
return mat.map(row => row[i]);
}
let colMaxes = [];
for (let i = 0; i < shape[1]; i++) {
colMaxes.push(Math.max.apply(null, col(mat, i).map(n => n.toString().length)));
}
mat.forEach((row, rowIdx) => {
console.log.apply(null, row.map((val, j) => {
if (val === 0) val = '-';
if(path.length != 0) {
if(path.includes('' + rowIdx + j)) val = '*'
}
if (rowIdx === 0 && j == 0) val = 'S';
if (rowIdx === 7 && j == 7) val = '⭐';
return new Array(colMaxes[j]-val.toString().length+1).join(" ") + val.toString() + " ";
}));
});
}$ node shortest-path-matrix.js
S - - - 1 - 1 -
1 - 1 - - - - -
- - - 1 1 1 - -
- - - - - 1 - 1
- 1 1 1 - 1 - -
- - - - - 1 - 1
- 1 1 1 1 1 - -
- - - - - - - ⭐
starting position: [ 0, 0 ]
target position: [ 7, 7 ]
queue: [ [ 0, 0 ] ]
current node (row, col): 0 0
======================= new queue item ====
queue: [ [ 0, 1 ] ]
current node (row, col): 0 1
...
======================= new queue item ====
queue: [ [ 7, 6 ], [ 6, 7 ], [ 7, 5 ] ]
current node (row, col): 7 6
S * * * 1 - 1 -
1 - 1 * * * * -
- - - 1 1 1 * -
- - - - - 1 * 1
- 1 1 1 - 1 * -
- - - - - 1 * 1
- 1 1 1 1 1 * -
- - - - - - * ⭐
[
'00', '01', '02', '03',
'13', '14', '15', '16',
'26', '36', '46', '56',
'66', '76', '77'
]How to think and solve problems with Breadth First Search
- Build graph & nodes data from given data.
- Shortest path with equal edge weight -> BFS.
- Examine the data with BFS pattern (level by level) to see if it solves your problem.
Summary
| Prob. class | P. sub-class | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|---|
| (almost) ANY problem class | array, matrix, ... | Brute Force | O(n) & up |
Can try with any problem type | - pass split test - array, string or graph, ... - divide, solve, combine gives a possible solution |
Divide and Conquer | O(nlogn) |
- accessing 2 data points at a time is useful- closing in the pointers proven to give a correct answer - usually array or string |
Two Pointers | O(n) |
| 1. Maximization 2. Minimization |
array, string or graph, ... | Greedy choice, no guarantee for most optimal solution |
varies |
|
| 3. Find all options | array, matrix, ... | Brute Force | O(n) & up |
|
| 4. Find most optimal solution | ||||
| 5. Find a truth | search for a number | - sorted array or balanced BST |
Binary Search | O(logn) |
| accessing a few consecutive data points at the same time is necessary/useful | - usually array or string | Slding Window | O(n) |
|
| - shortest path, equal edge weight - node visitation layer by layer |
- graph or matrix | Breadth First Search | O(n) |
|
Real life interview questions
- How does Breadth First Search solve problems?
- What kind of problems can typically be solved by Breadth First Search?
- Recalculate the Complexity of the three problems above.
- Redo the three problems above. You should be able to quickly explain how the algorithm works and implement each of them within 15 mins.
- From BFS matrix example above, construct a graph with adjacency list, then starting from
00, print layer by layer with|as layer separator. - (Easy) Leetcode #733. Flood Fill
- (Medium) Leetcode #695. Max Area of Island
- (Medium) Leetcode #200. Number of Islands
- (Medium) Leetcode #1267. Count Servers that Communicate
- (Medium) Leetcode #529. Minesweeper
- (Medium) Leetcode #743. Network Delay Time
- More on Leetcode #breadth-first-search.