Greedy algorithm

/
fundamentals

This tutorial is a part of the Data Structures and Algorithms class:

A typical problem solved by Greedy algorithm

  • Make the Greediest choice in current step and hope for the most optimal solution after all steps.
  • Also called: local optimal hopefully will also be global optimal. Sometimes it is, most times it isn't.
  • Greedy is too simple. It can only solve very simple problems. But problems are usually not simple.
  • Then why learn Greedy? Popularity, historical reason, before better algo (DP for ex) comes along.

greedy algo

lecture-21/coin-change.js
// return the minimum number of coins to sum up to a given sum

const greedy = (coins, sum) => {
  coins.sort((a, b) => b - a) // O(nlogn)

  console.log('coins:', coins)
  console.log('sum:', sum)
  
  const result = {}
  let sumRemain = sum

  for(let i = 0; i < coins.length; i++) { // O(n)
    const numCoin = Math.floor(sumRemain/coins[i])
    if(numCoin > 0) {
      result[coins[i] + ' coin(s)'] = numCoin
      sumRemain = sumRemain - numCoin * coins[i]
    }
  }

  result.sumRemain = sumRemain

  return result
}

console.log(JSON.stringify(greedy([1, 2, 5], 21), null, 4));
console.log('========================')
console.log(JSON.stringify(greedy([2, 5], 21), null, 4));

// Time complexity: O(nlogn), with n is number of coin types
$ node coin-change.js
coins: [ 5, 2, 1 ]
sum: 21
{
    "5 coin(s)": 4,
    "1 coin(s)": 1,
    "sumRemain": 0
}
========================
coins: [ 5, 2 ]
sum: 21
{
    "5 coin(s)": 4,
    "sumRemain": 1
}

Characteristics of problems can be solved by Greedy

  • Not recommended to use in coding interview. Can use in real life application if no choice left.
Problem Input characteristics Algorithm Time Complexity
Maximization, Minimization - usually array, string or graph Greedy choice,
no guarantee for most optimal solution		 varies

gready max path

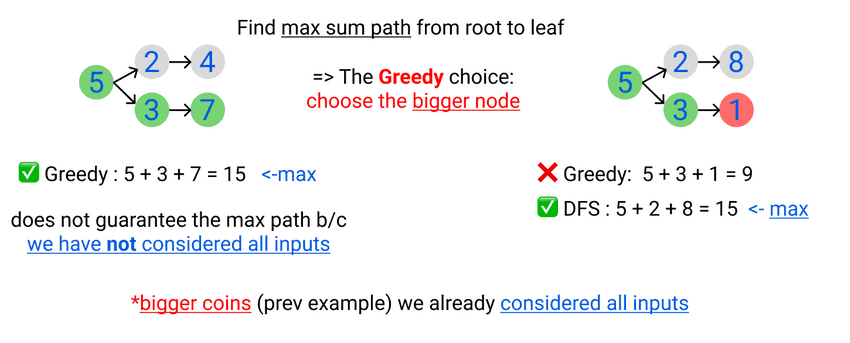
lecture-21/max-sum-path.js
// Find max sum path from root to leaf

// structure of a node
class Node {
  constructor(data) {
    this.data = data
    this.left = null
    this.right = null
  }
}

// Binary Tree
class BinaryTree {
  constructor(data) {
    this.root = data ? new Node(data) : null
  }
}

// create new binary tree
const binaryTree = new BinaryTree()
binaryTree.root = new Node(5) // add root node, 5

// add level 1 nodes: 3, 2
binaryTree.root.left = new Node(3)
binaryTree.root.right = new Node(2)

// add level 2 nodes: 7, 4
binaryTree.root.left.left = new Node(7)
binaryTree.root.right.right = new Node(4)
console.log(JSON.stringify(binaryTree, null, 4))

const sum1 = { max: 0 }

const greedySumPath = (node, sum) => {
  if(!node) return sum

  sum.max = sum.max + node.data

  if(node.left?.data >= node.right?.data || node.left?.data && !node.right?.data) {
    console.log('next node on left:', node.left.data)
    greedySumPath(node.left, sum)
  }
  
  if(node.left?.data < node.right?.data || node.right?.data && !node.left?.data) {
    console.log('next node on right:', node.right.data)
    greedySumPath(node.right, sum)
  }

  return sum
}

// Time complexity: worst case O(n), n is total number of nodes

console.log(greedySumPath(binaryTree.root, sum1))


console.log('========================')


// create new binary tree
const binaryTree2 = new BinaryTree()
binaryTree2.root = new Node(5)
binaryTree2.root.left = new Node(3)
binaryTree2.root.right = new Node(2)
binaryTree2.root.left.left = new Node(1)
binaryTree2.root.right.right = new Node(8)
console.log(JSON.stringify(binaryTree2, null, 4))


const sum2 = { max: 0 }
console.log(greedySumPath(binaryTree2.root, sum2))
$ node max-sum-path.js
{
    "root": {
        "data": 5,
        "left": {
            "data": 3,
            "left": {
                "data": 7,
                "left": null,
                "right": null
            },
            "right": null
        },
        "right": {
            "data": 2,
            "left": null,
            "right": {
                "data": 4,
                "left": null,
                "right": null
            }
        }
    }
}
next node on left: 3
next node on left: 7
{ max: 15 }
========================
{
    "root": {
        "data": 5,
        "left": {
            "data": 3,
            "left": {
                "data": 1,
                "left": null,
                "right": null
            },
            "right": null
        },
        "right": {
            "data": 2,
            "left": null,
            "right": {
                "data": 8,
                "left": null,
                "right": null
            }
        }
    }
}
next node on left: 3
next node on left: 1
{ max: 9 }

Summary

Prob. class P. sub-class Input characteristics Algorithm Time
Complexity
(almost) ANY problem class array, matrix, ... Brute Force O(n) & up
1. Maximization
2. Minimization		 array, string or graph, ... Greedy choice,
no guarantee for most optimal solution		 varies
3. Find all options array, matrix, ... Brute Force O(n) & up
4. Find most optimal solution
5. Find a truth search for a number - sorted array
or balanced BST		 Binary Search O(logn)

Real life interview questions

All problems below can be solved without Greedy algorithm. You can solve them by logical thinking and are not forced to use Greedy. However, thinking about a Greedy approach (if possible) is encouraged afterward.

  1. Greedy is a simple algorithm. Why is it simple and how does Greedy solve problems?
  2. What kind of problems can be typically solved by Greedy?
  3. (Easy) Leetcode #561: Array Partition
  4. (Easy) Leetcode #2160: Minimum Sum of Four Digit Number After Splitting Digits
  5. (Easy) Leetcode #2099: Find Subsequence of Length K With the Largest Sum
  6. (Easy) Leetcode #1323: Maximum 69 Number
  7. (Easy) Leetcode #1827: Minimum Operations to Make the Array Increasing
  8. (Medium) Leetcode #763: Partition Labels
  9. Solve all problems above, including the two from the tutorial with recursion/loop.
  10. More on Leetcode #greedy. Progress check: you should be fairly comfortable doing any of problems in related subject after finishing all problems above.