This tutorial is a part of the Data Structures and Algorithms class:
- A typical problem solved by Two Pointers algorithm
- Characteristics of problems can be solved by Two Pointers
- Summary
A typical problem solved by Two Pointers algorithm
- Two pointers algorithm gives us access to
2data points at a time. - One pointer will move at a time toward the other pointer.
- The solution is only correct when the logic of moving the pointers will not miss any meaningful data points.
| For Loop | Binary Search | Two Pointers | |
|---|---|---|---|
| # of data point(s) access | 1 |
1 |
2 |
| Time Complexity | O(n) |
O(logn) |
O(n) |
| Special requirement | - | (must) sorted array | (optional) sorted array |

lecture-24/three-sum.js
// Find 3 nums in an array that adds up to a sum
// Time complexity: O(n^3)
const threeSumForLoops = (nums, sum) => {
const result = []
for(let i = 0; i < nums.length; i++) { // pick 1st num
for(let j = i + 1; j < nums.length; j++) { // pick 2nd num
for(let k = j + 1; k < nums.length; k++) { // pick 3rd num
if(nums[i] + nums[j] + nums[k] === sum) {
result.push([nums[i], nums[j], nums[k]])
}
}
}
}
return result
}
// Time complexity: O(n^2logn)
const threeSumForLoopsAndBinarySearch = (nums, sum) => {
nums.sort((a, b) => a - b) // O(nlogn)
const result = []
for(let i = 0; i < nums.length; i++) { // pick 1st num
for(let j = i + 1; j < nums.length; j++) { // pick 2nd num
let remain = sum - nums[i] - nums[j]
let left = j + 1
let right = nums.length - 1
while(left <= right) { // pick 3rd num, Binary Search
let mid = Math.floor((left + right) / 2)
if(nums[mid] === remain) {
result.push([nums[i], nums[j], nums[mid]])
break
} else if(nums[mid] > remain) {
right--
} else {
left++
}
}
}
}
return result
}
// Time complexity: O(n^2)
const threeSumTwoPointers = (nums, sum) => {
const result = []
nums.sort((a,b) => a-b) // O(nlogn)
for(let i = 0; i < nums.length; i++) { // pick 1st num
let left = i + 1
let right = nums.length - 1
while(left < right) { // pick 2nd + 3rd, two pointers
let current = nums[i] + nums[left] + nums[right]
if(current === sum) { // found target sum
result.push([nums[i], nums[left], nums[right]])
break
} else if(current > sum) { // current sum bigger than target,
right-- // move right pointer to the left
} else { // current sum smaller than target,
left++ // move left pointer to the right
}
}
}
return result
}
console.log('3 For loops:')
console.log(threeSumForLoops([15, 26, 13, 7, 3, 5, 2, 22], 30))
console.log('2 For loops + Binary Search:')
console.log(threeSumForLoopsAndBinarySearch([15, 26, 13, 7, 3, 5, 2, 22], 30))
console.log('1 For loop + Two Pointers:')
console.log(threeSumTwoPointers([15, 26, 13, 7, 3, 5, 2, 22], 30))$ node three-sum.js
3 For loops:
[ [ 15, 13, 2 ], [ 3, 5, 22 ] ]
2 For loops + Binary Search:
[ [ 2, 13, 15 ], [ 3, 5, 22 ] ]
1 For loop + Two Pointers:
[ [ 2, 13, 15 ], [ 3, 5, 22 ] ]Characteristics of problems can be solved by Two Pointers
- Using and implementing Two Pointers is very simple.
- Quickly try and see if it solves your problem is the best way to use it.
| Problem | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|
Accessing 2 data points at a time is useful |
- closing in the pointers proven to give a correct answer - usually array or string |
Two Pointers | O(n) |
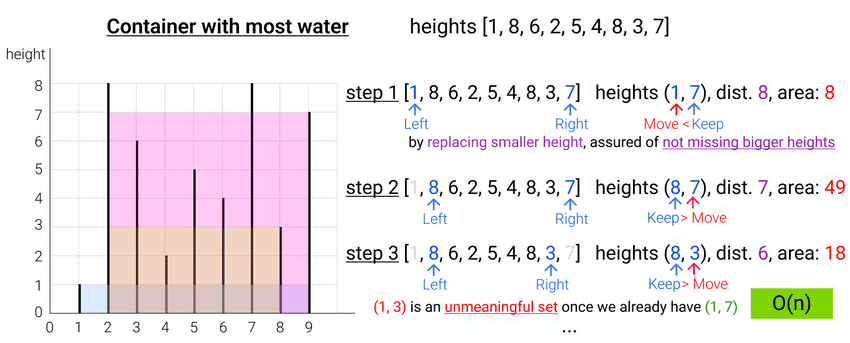
lecture-24/container-with-most-water.js
// Find container with most water
// Time Complexity: O(n)
const maxArea = (height) => {
let left = 0
let right = height.length - 1
let curMax = 0
while (left < right) { // Two Pointers
let newArea = (right - left) * Math.min(height[left], height[right])
curMax = Math.max(curMax, newArea)
console.log(
'height left:', height[left],
'right:', height[right],
'dist:', right - left,
'area:', newArea
)
// move the pointer where height is smaller
if (height[left] > height[right]) { // move right pointer to the left
right--
} else { // move left pointer to the right
left++
}
}
return curMax
}
console.log('max area:', maxArea([1,8,6,2,5,4,8,3,7])) // max area: 49$ node container-with-most-water.js
height left: 1 right: 7 dist: 8 area: 8
height left: 8 right: 7 dist: 7 area: 49
height left: 8 right: 3 dist: 6 area: 18
height left: 8 right: 8 dist: 5 area: 40
height left: 6 right: 8 dist: 4 area: 24
height left: 2 right: 8 dist: 3 area: 6
height left: 5 right: 8 dist: 2 area: 10
height left: 4 right: 8 dist: 1 area: 4
max area: 49Summary
| Prob. class | P. sub-class | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|---|
| (almost) ANY problem class | array, matrix, ... | Brute Force | O(n) & up |
Can try with any problem type | - pass split test - array, string or graph, ... - divide, solve, combine gives a possible solution |
Divide and Conquer | O(nlogn) |
- accessing 2 data points at a time is useful- closing in the pointers proven to give a correct answer - usually array or string |
Two Pointers | O(n) |
| 1. Maximization 2. Minimization |
array, string or graph, ... | Greedy choice, no guarantee for most optimal solution |
varies |
|
| 3. Find all options | array, matrix, ... | Brute Force | O(n) & up |
|
| 4. Find most optimal solution | ||||
| 5. Find a truth | search for a number | - sorted array or balanced BST |
Binary Search | O(logn) |
Real life interview questions
- How does Two Pointers solve problems?
- What kind of problems can typically be solved by Two Pointers?
- Redo the two problems above. You should be able to quickly explain how the algorithm works and implement each of them within 15 mins.
- (Medium) Leetcode #167. Two Sum II - Input Array Is Sorted
- (Medium) Leetcode #15. 3Sum
- (Medium) Leetcode #18. 4Sum
- (Easy) Leetcode #344. Reverse String
- (Easy) Leetcode #125. Valid Palindrome
- (Medium) Leetcode #189. Rotate Array
- (Medium) Leetcode #11. Container With Most Water
- More on Leetcode #two-pointers.