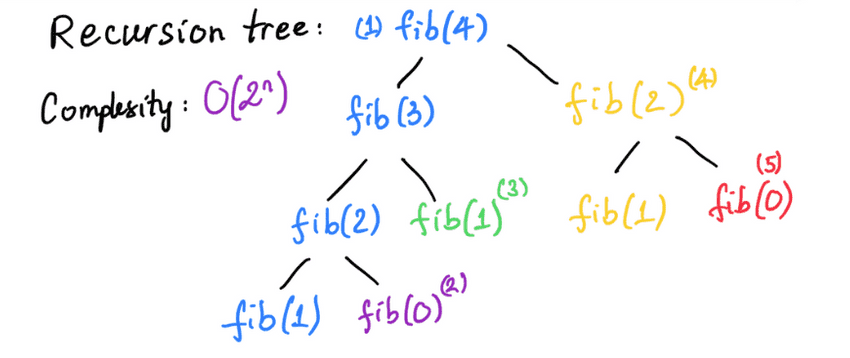Recursion, FOR/WHILE LOOP with some overhead

/
fundamentals

*Prerequisite: Understanding function call stack and recursion.

This tutorial is a part of the Data Structures and Algorithms class:

Recursion is simply a FOR/WHILE LOOP

  • Recursion is one of the most scary things for most software engineers. Not after today!
  • Recursion is simply applying the same function (processing) with different data.
  • We think of Recursion as a FOR/WHILE LOOP. And we use Recursion as a FOR/WHILE LOOP.
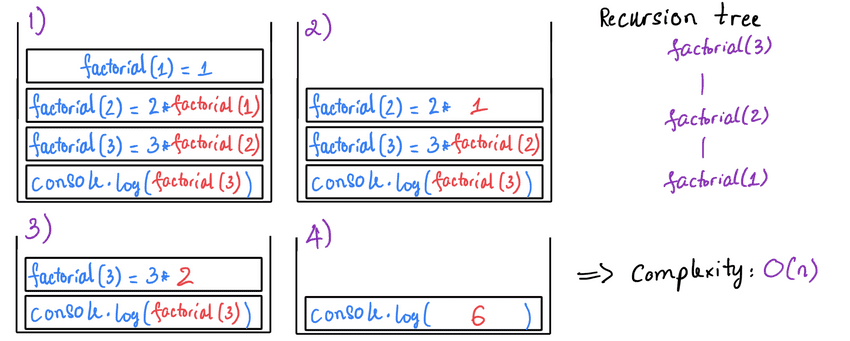
  • Whenever we see recursion in a calculation, ex: n * factorial(n - 1), immediately go to the bottom base case and think up (bottom up). The calculation always waits for the base case.
lecture-11/recursion-factorial.js
// function to return factorial (n!) of a given number `n`
const factorial = (n) => {
  console.log('n:', n)
  if(n === 1) return 1
  return n * factorial(n - 1)
}
// 3! = 3 * 2 * 1 = 6
console.log(factorial(3)) // 6, [all cases stack up to WAIT FOR BASE CASE OUTPUT]

factorial recursion

Recursion is a FOR/WHILE LOOP with some overhead

  • The recursion function itself is where we process one data point.
  • Calling the function again with different data (recursive call) is to process the next data point.
  • Similarities and differences between Recursion and LOOP (with examples):
Uses Recursion LOOP Example
Loop through data points: array, string, matrix, graph ✅ ✅ 1, 2, 3
How to move on to the next data point call function again with new data (Recursive call) syntax 1, 2, 3
How to exit the loop Base case(s) index condition 1, 2, 3
Process data while looping ✅ ✅ 1, 2
Process data from the end (bottom up)* ✅ ✅ 3
Does not open a lot nested, scoped functions ❌ overhead ✅ 1, 2, 3
Does not limit max number of data points by callstack size ❌ overhead ✅ 1, 2, 3
RAM and CPU more efficient ❌ overhead ✅ 1, 2, 3

Any capability to process data that Recursion has, LOOP has it.

Conclusion: Every recursion solution has a (for/while) loop solution and vice versa. But always remember recursion is not as efficient, and max data size is limited by callstack size.

Example 1: find max integer from array

lecture-19/recursion-is-a-for-loop.js
// Find max element in given array
const arr = [2, 4, 3, 9, 1]

console.log('==== equivalent FOR LOOP solution ====')

const findMaxForLoop = arr => {
  let curMax = arr[0]

  for(let i = 0; i < arr.length; i++) {
    console.log('i:', i, ',', 'arr[i]:', arr[i])
    ;(arr[i] > curMax) && (curMax = arr[i])
  }

  return curMax
}

console.log('Max, FOR LOOP solution:', findMaxForLoop(arr)) // 9
// Time complexity: O(n)


console.log('==== equivalent Recursion solution ====')

// save max to curMaxObj.max
let curMaxObj = { max : arr[0] }

const findMaxRecursion = (arr, i, curMaxObj) => {

  // logging to see current `i` and `arr[i]`
  console.log('i:', i, ',', 'arr[i]:', arr[i])

  // exit condition aka base case
  if (i >= arr.length) return
  
  // process current data point
  if(arr[i] > curMaxObj.max) { curMaxObj.max = arr[i] }
  console.log('curMax:', curMaxObj.max)

  // continue to loop
  findMaxRecursion(arr, i+1, curMaxObj)
}

findMaxRecursion(arr, 0, curMaxObj)

console.log('Max, Recursion solution:', curMaxObj.max) // 9
// Time complexity: O(n)
$ node recursion-is-a-for-loop.js
==== equivalent FOR LOOP solution ====
i: 0 , arr[i]: 2
i: 1 , arr[i]: 4
i: 2 , arr[i]: 3
i: 3 , arr[i]: 9
i: 4 , arr[i]: 1
Max, FOR LOOP solution: 9
==== equivalent Recursion solution ====
i: 0 , arr[i]: 2
curMax: 2
i: 1 , arr[i]: 4
curMax: 4
i: 2 , arr[i]: 3
curMax: 4
i: 3 , arr[i]: 9
curMax: 9
i: 4 , arr[i]: 1
curMax: 9
i: 5 , arr[i]: undefined
Max, Recursion solution: 9

Example 2: loop through data points in binary tree

lecture-19/recursion-loops-through-graph.js
// structure of a node
class Node {
  constructor(data) {
    this.data = data
    this.left = null
    this.right = null
  }
}

// Binary Tree
class BinaryTree {
  constructor(data) {
    this.root = data ? new Node(data) : null
  }
}

// create new binary tree
const binaryTree = new BinaryTree(6)
binaryTree.root.left = new Node(4)
binaryTree.root.left.left = new Node(1)
binaryTree.root.left.right = new Node(5)
binaryTree.root.right = new Node(8)
binaryTree.root.right.right = new Node(10)

console.log(JSON.stringify(binaryTree, null, 4))

console.log('==== equivalent WHILE LOOP solution ====')

const traverseWithWhileAndQueue = (root) => { // aka Breadth First Search
  const queue = [root]
  const result = []
  let loopCount = 1

  console.log('initial queue data: ', queue[0].data)

  while(queue.length > 0) {
    console.log('loop #:', loopCount)
    loopCount++

    const queueData = queue.map(e => e.data )
    console.log('queue data: ', queueData)

    const currentNode = queue.shift() // dequeue

    currentNode.left && queue.push(currentNode.left) // enqueue
    currentNode.right && queue.push(currentNode.right) // enqueue

    result.push(currentNode.data) // process current node data
    console.log('result: ', result)
    console.log('- - - - - - - - -')
  }
}

traverseWithWhileAndQueue(binaryTree.root)
// Time complexity: O(n)

console.log('==== equivalent Recursion solution ====')

const queue = [binaryTree.root]
const result = []
let loopCount = 1

const traverseWithRecursion = (queue) => { // aka Breadth First Search
  if (queue.length == 0) return
  
  console.log('loop #:', loopCount)
  loopCount++

  const queueData = queue.map(e => e.data )
  console.log('queue data: ', queueData)

  const currentNode = queue.shift() // dequeue

  currentNode.left && queue.push(currentNode.left) // enqueue
  currentNode.right && queue.push(currentNode.right) // enqueue

  result.push(currentNode.data) // process current node data
  console.log('result: ', result)
  console.log('- - - - - - - - -')
  traverseWithRecursion(queue)
}

traverseWithRecursion(queue)
// Time complexity: O(n)
$ node recursion-loops-through-graph.js
{
    "root": {
        "data": 6,
        "left": {
            "data": 4,
            "left": {
                "data": 1,
                "left": null,
                "right": null
            },
            "right": {
                "data": 5,
                "left": null,
                "right": null
            }
        },
        "right": {
            "data": 8,
            "left": null,
            "right": {
                "data": 10,
                "left": null,
                "right": null
            }
        }
    }
}
==== equivalent WHILE LOOP solution ====
initial queue data:  6
loop #: 1
queue data:  [ 6 ]
result:  [ 6 ]
- - - - - - - - -
loop #: 2
queue data:  [ 4, 8 ]
result:  [ 6, 4 ]
- - - - - - - - -
loop #: 3
queue data:  [ 8, 1, 5 ]
result:  [ 6, 4, 8 ]
- - - - - - - - -
loop #: 4
queue data:  [ 1, 5, 10 ]
result:  [ 6, 4, 8, 1 ]
- - - - - - - - -
loop #: 5
queue data:  [ 5, 10 ]
result:  [ 6, 4, 8, 1, 5 ]
- - - - - - - - -
loop #: 6
queue data:  [ 10 ]
result:  [ 6, 4, 8, 1, 5, 10 ]
- - - - - - - - -
==== equivalent Recursion solution ====
loop #: 1
queue data:  [ 6 ]
result:  [ 6 ]
- - - - - - - - -
loop #: 2
queue data:  [ 4, 8 ]
result:  [ 6, 4 ]
- - - - - - - - -
loop #: 3
queue data:  [ 8, 1, 5 ]
result:  [ 6, 4, 8 ]
- - - - - - - - -
loop #: 4
queue data:  [ 1, 5, 10 ]
result:  [ 6, 4, 8, 1 ]
- - - - - - - - -
loop #: 5
queue data:  [ 5, 10 ]
result:  [ 6, 4, 8, 1, 5 ]
- - - - - - - - -
loop #: 6
queue data:  [ 10 ]
result:  [ 6, 4, 8, 1, 5, 10 ]
- - - - - - - - -

Example 3: process data bottom up

lecture-19/recursion-process-data-bottom-up.js
// Calculate Fibonacci number at position `n`

console.log('==== equivalent FOR LOOP solution ====')

const fibForLoop = (n) => {
  let fn_2 = 0 // f(0)
  let fn_1 = 1 // f(1)
  
  if(n === 0) return fn_2
  if(n === 1) return fn_1

  let fn = 0

  for(let i = 2; i <= n; i++) {
    fn = fn_1 + fn_2 // f(n) = f(n-1) + f(n-2)
    fn_2 = fn_1
    fn_1 = fn
  }
  
  return fn
}

console.log(fibForLoop(10)) // 55
// Time complexity: O(n)

console.log('==== equivalent Recursion solution ====')

const fibRecursion = (n) => {
  if(n === 1) return 1
  if(n === 0) return 0
  return fibRecursion(n-1) + fibRecursion(n-2)
}

console.log(fibRecursion(10)) // 55
// Time complexity: O(2^n)

fib recursion 

$ node recursion-process-data-bottom-up.js
==== equivalent FOR LOOP solution ====
55
==== equivalent Recursion solution ====
55

Use recursion in your algorithm: bottom up or along the way

  • Just think of Recursion as a loop. Nothing more!
  • If your solution depends on bottom up values (base cases) -> recursion can make the code shorter, but the complexity higher.
  • Recursion adds a flexibility to continue the loop by directly passing new data to the call. It does not need an index. Which is why a lot of the time, when dealing with graph data, you might see a lot of recursion.
  • LOOP is usually more optimized than Recursion.

factorial recursion

Note: Understanding recursion and how to use it is key to understand algorithms we'll learn later. Make sure you understand the similarities and differences between Recursion and LOOP. And you can interchangingly use them at ease.

It's simple to understand but you gotta practice and redo these examples many times. Then when understood, do the real life interview questions below.

Real life interview questions

  1. What are the differences between Recursion and LOOP?
  2. In example 1, Recusion solution, instead of passing curMaxObj as a object, try passing a literal (number), see if you can get the result you want. Explain why/why not?
  3. Solve all problems below in both Recursion and LOOP. Then compare the complexities of your algorithms.
  4. Given a random 4x4 matrix, print all elements. Row by row and column by column.
  5. Redo While and Stack tree traversal with Recursion.
  6. Leetcode #344: Reverse String
  7. Leetcode #394: Decode String
  8. Leetcode #206: Reverse Linked List
  9. Leetcode #203: Remove Linked List Elements
  10. Leetcode #234: Palindrome Linked List
  11. Leetcode #125: Valid Palindrome
  12. Leetcode #231: Power of Two
  13. Leetcode #326: Power of Three
  14. Leetcode #390: Elimination Game
  15. Leetcode #1823: Find the Winner of the Circular Game
  16. Bottom up: find factorial of a given number n! by yourself.
  17. Bottom up: Leetcode #509: Fibonacci Number
  18. Bottom up: Leetcode #104: Maximum Depth of Binary Tree