*Prerequisite: Tree data structure part 4/5: understanding function call stack and recursion.
This tutorial is a part of the Data Structures and Algorithms class:
- Extracting useful information from tree with recursion
- PreOrder traversal
- InOrder traversal
- PostOrder traversal
- PreOrder, InOrder, PostOrder traversal summary
- How fast to insert/delete/access/search data
- Algorithms: how to extract useful information out of input
Extracting useful information from tree with recursion
At this point, you should have a pretty good understanding how function call stack and recursion works. We will now apply this knowledge to extract useful information from tree by using recursion. Reminder:
| Human thought | Human action | Equivalent computer execution |
|---|---|---|
| looking at data | see the whole tree at a time | look at one node at a time + apply logic to only current node + use loop/recursion to visit all nodes |
| node selection | freely select nodes as asked | use Stack or Queue or change position of recursive call to control the order of node selection |
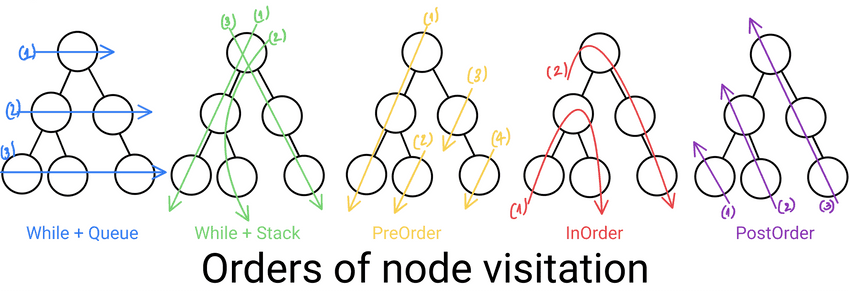
Traverse means walk, tree traversal means walking the tree. Tree traversal is just a fancy name for tree node visitation in a particular order. With recursion, we have 3 popular, official traversal names: PreOrder, InOrder and PostOrder traversal.
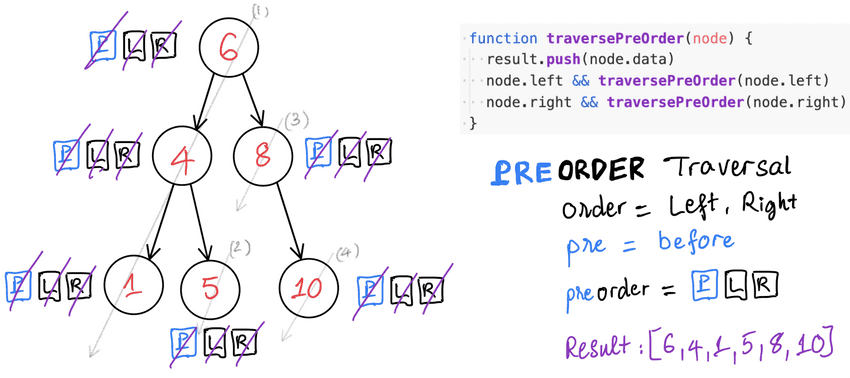
PreOrder traversal
Usefulness of this order of node visitation: whenever it gives value to your application.
// Binary Search Tree, without self-balancing
class BinarySearchTree {
// ...
// preorder traversal
preOrder() {
if (this.root == null) {
return null
} else {
var result = []
traversePreOrder(this.root)
return result
function traversePreOrder(node) {
result.push(node.data)
node.left && traversePreOrder(node.left)
node.right && traversePreOrder(node.right)
}
}
}
// ...
}$ node binary-search-tree-data-structure.js
preOrder(): [ 6, 4, 1, 5, 8, 10 ]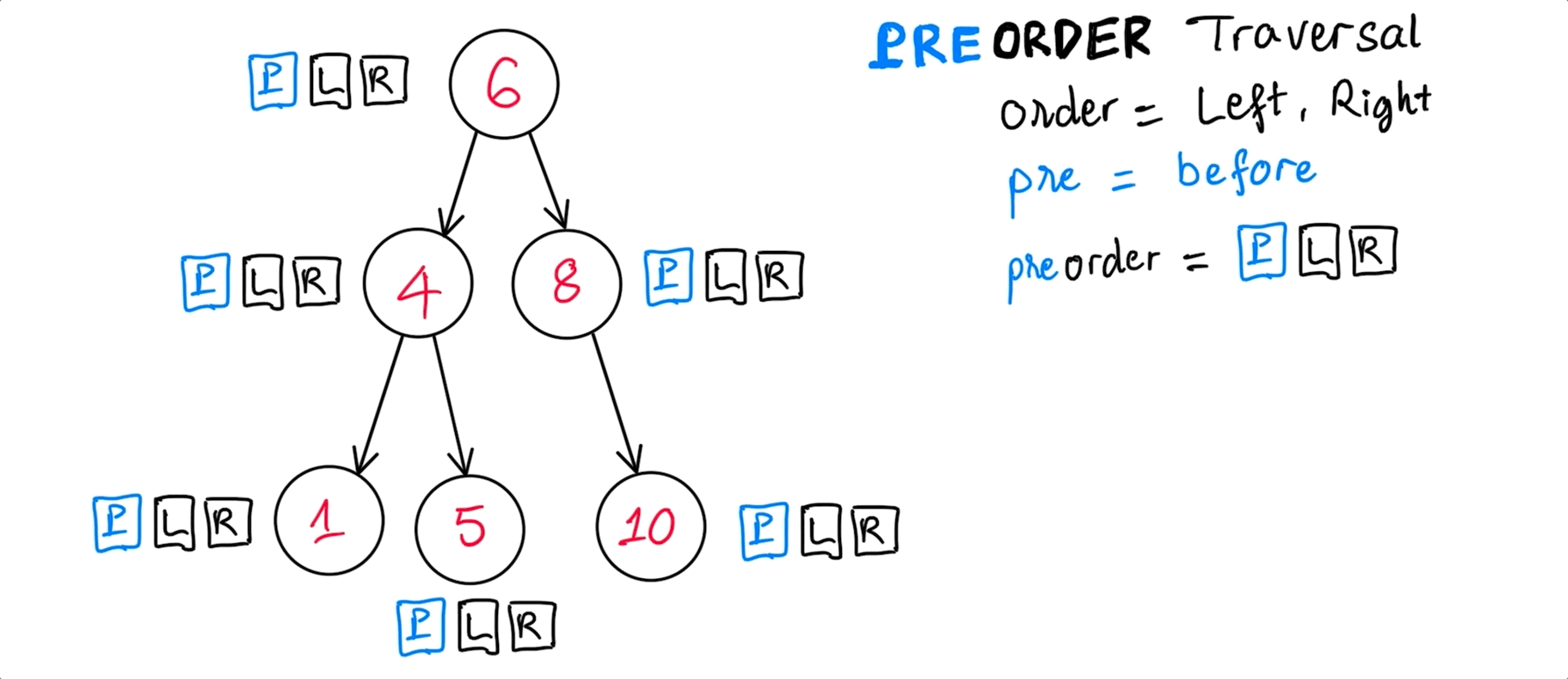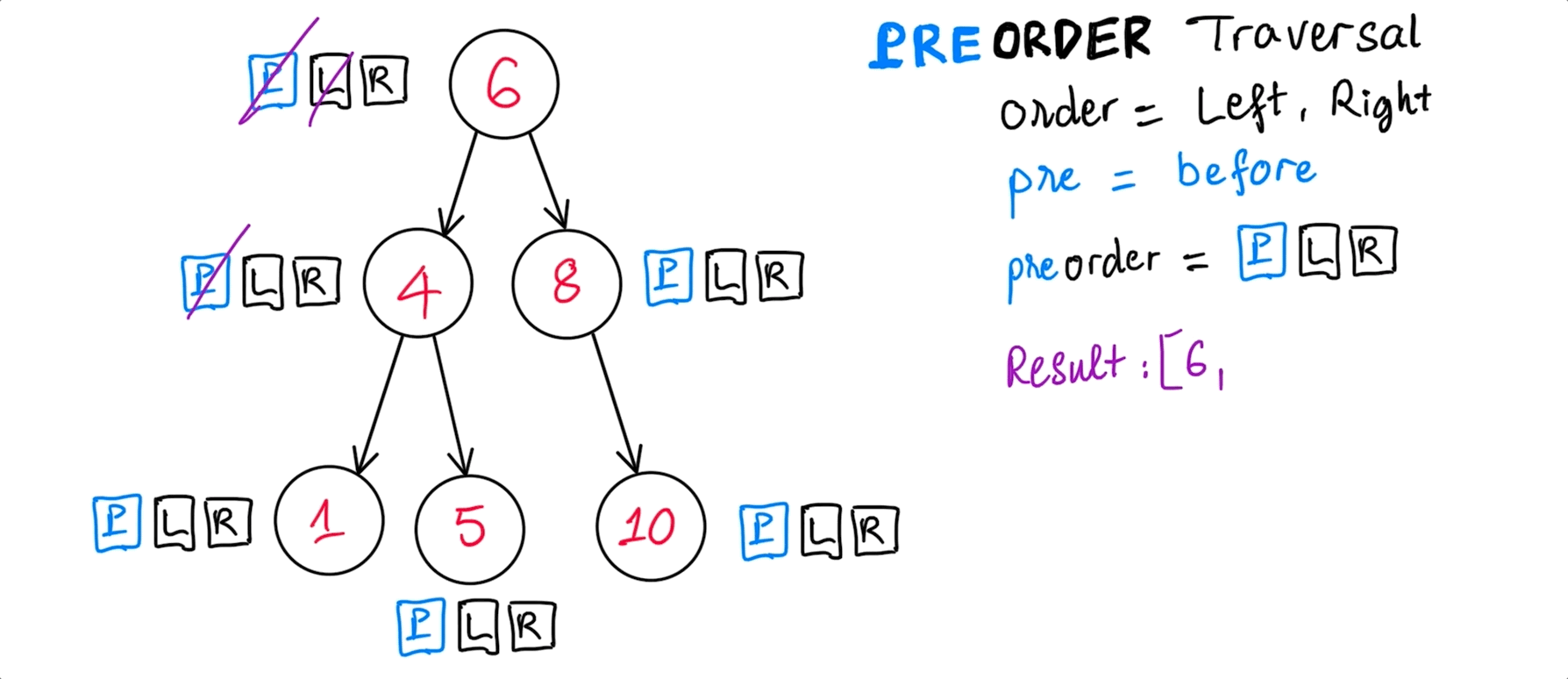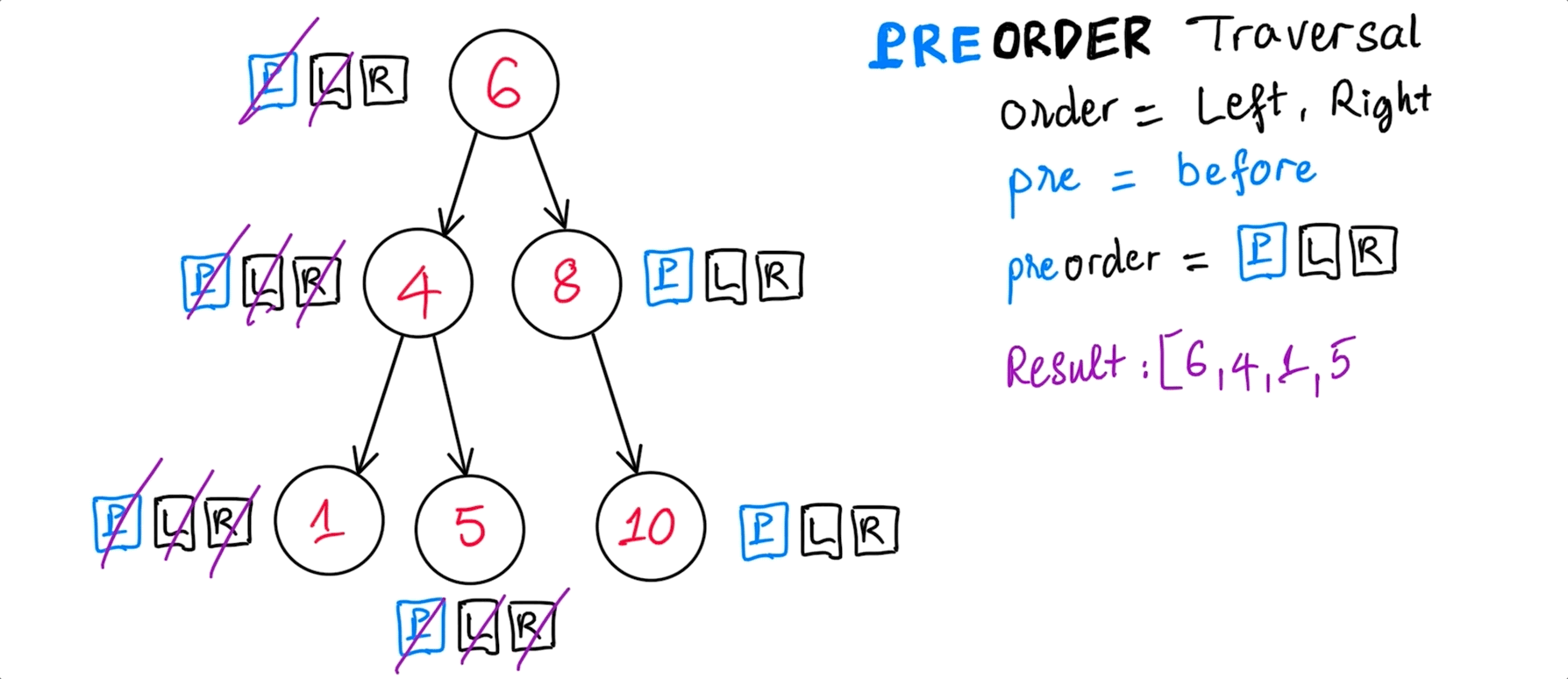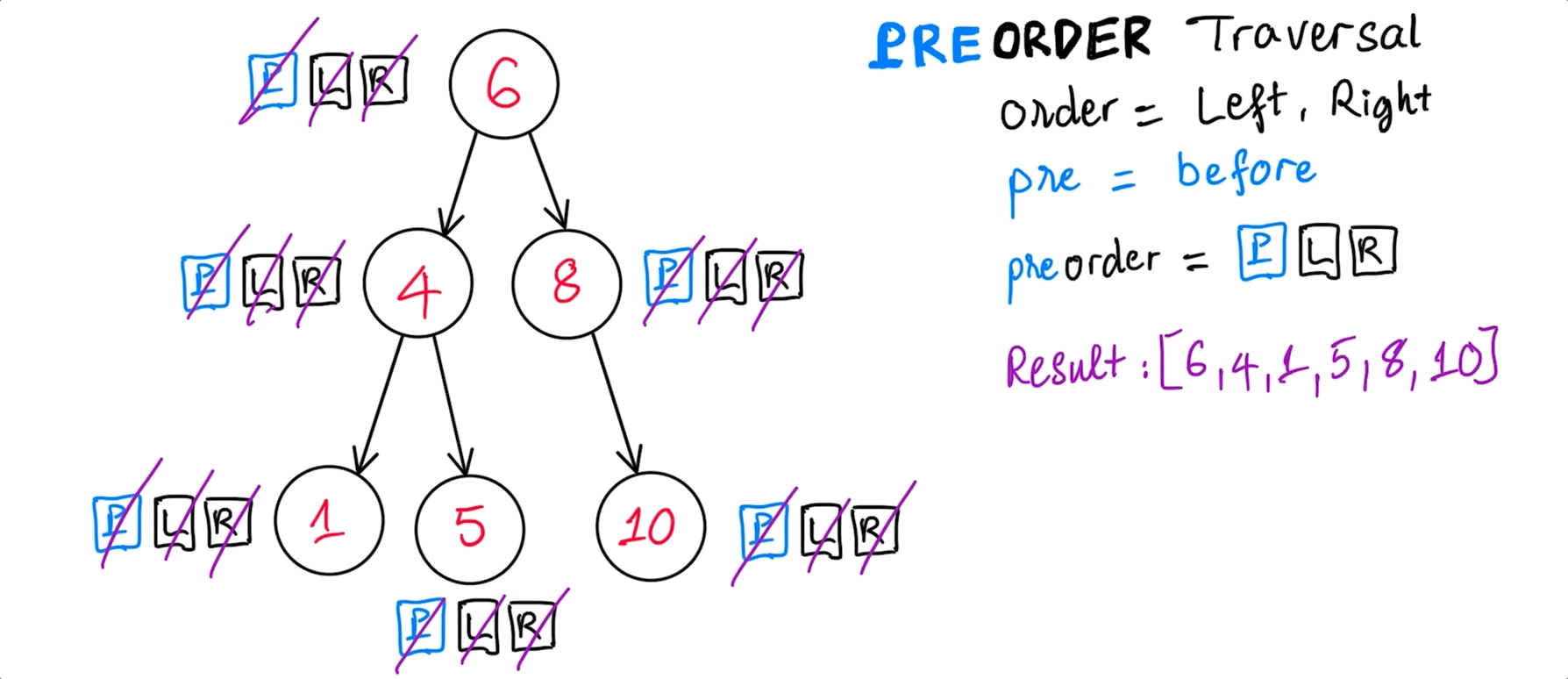
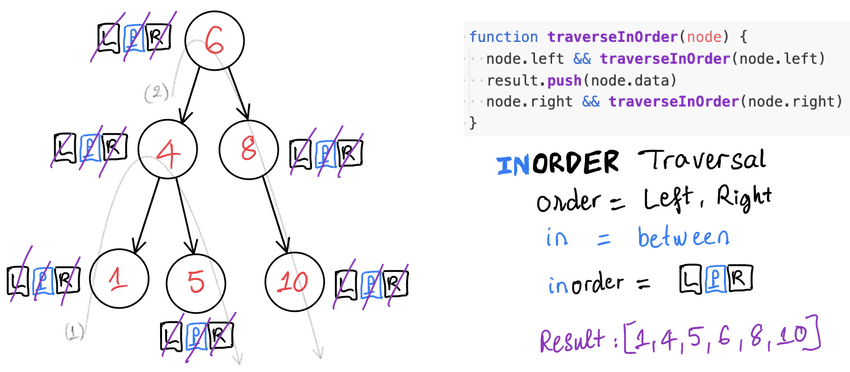
InOrder traversal
Usefulness of this order of node visitation: BST print min -> max and whenever it gives value to your application.
// Binary Search Tree, without self-balancing
class BinarySearchTree {
// ...
// inorder traversal (print min -> max)
inOrder() {
if (this.root == null) {
return null
} else {
var result = []
traverseInOrder(this.root)
return result
function traverseInOrder(node) {
node.left && traverseInOrder(node.left)
result.push(node.data)
node.right && traverseInOrder(node.right)
}
}
}
// ...
}$ node binary-search-tree-data-structure.js
inOrder(): [ 1, 4, 5, 6, 8, 10 ]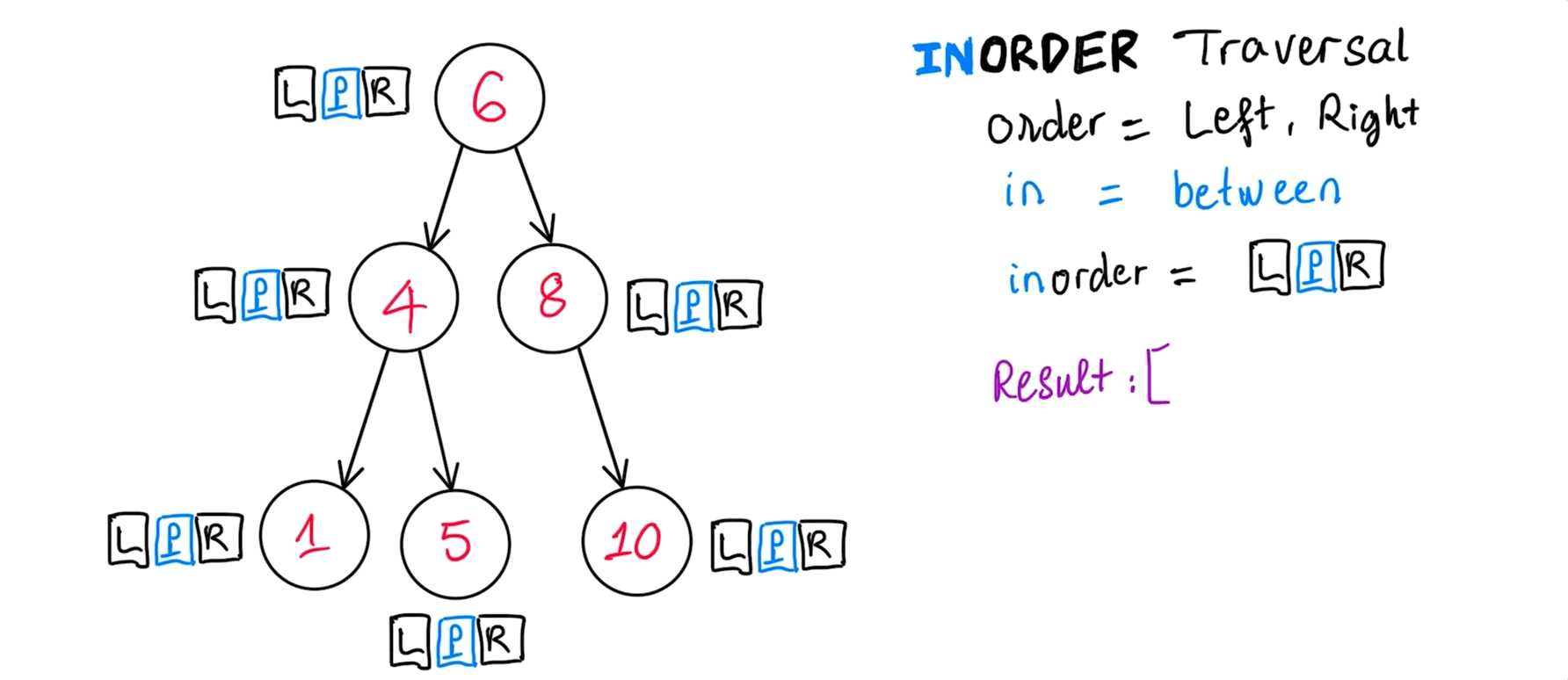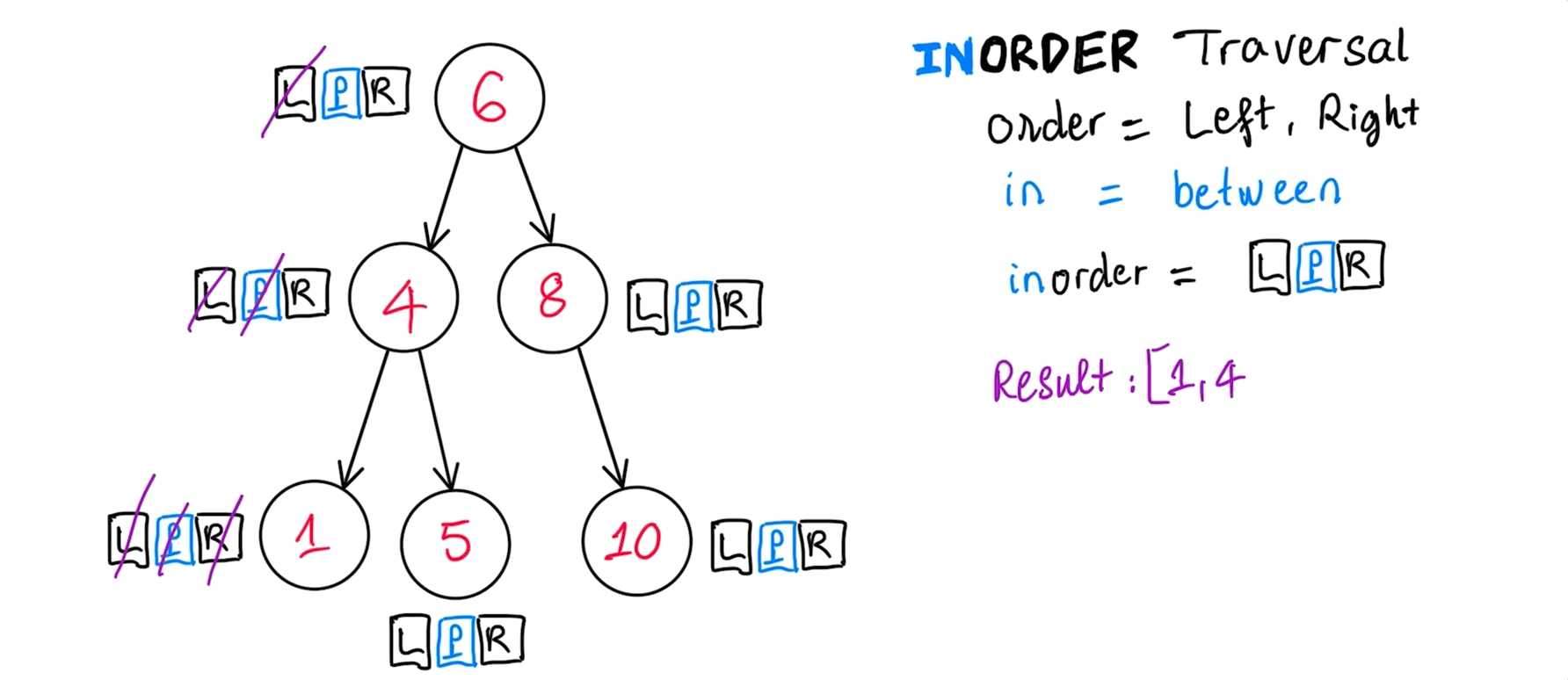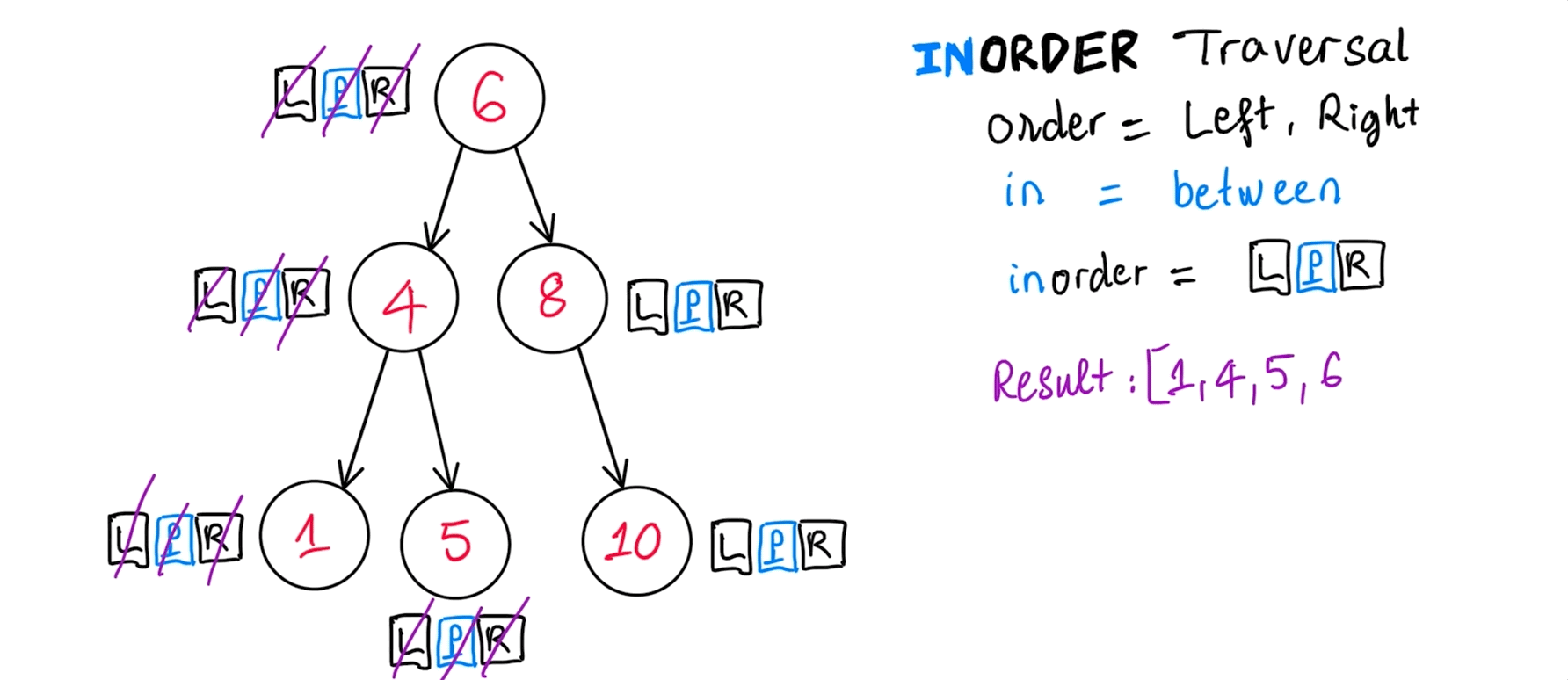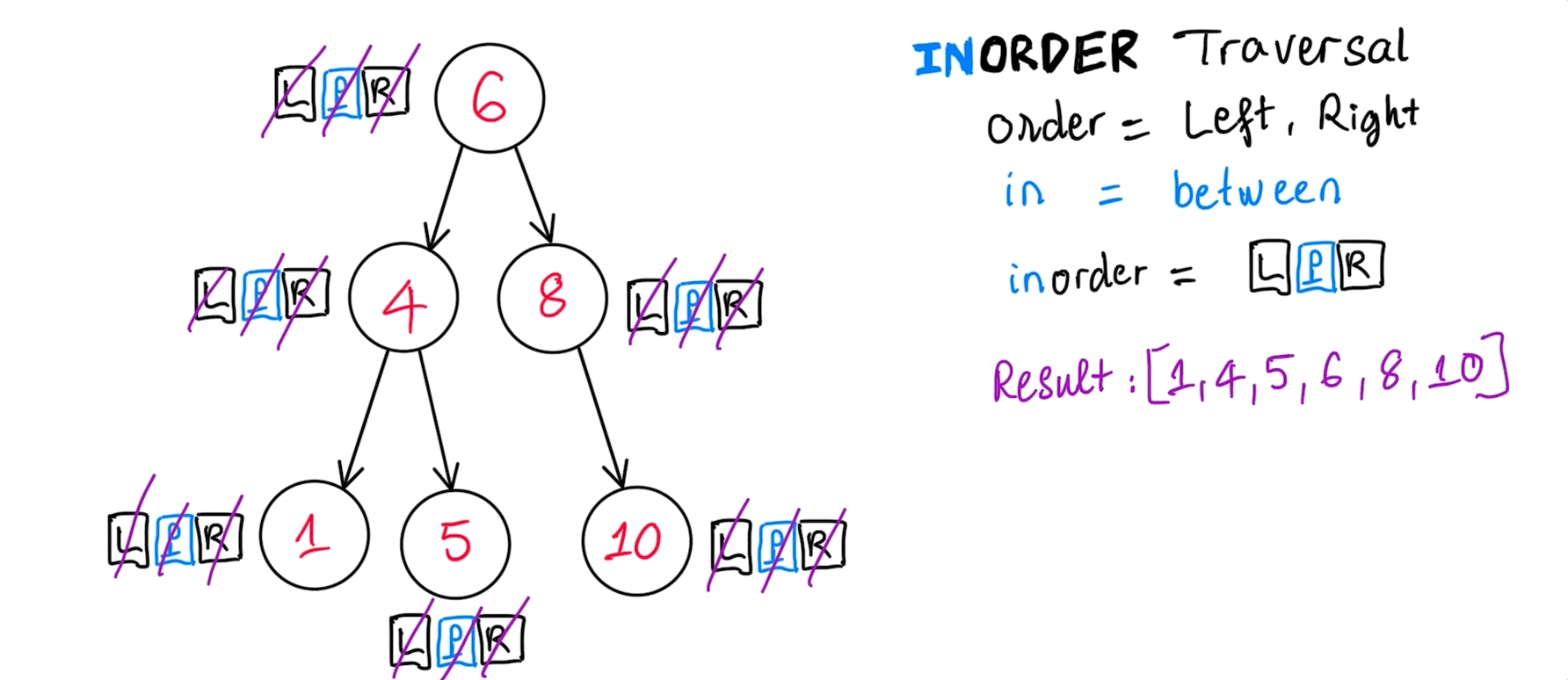
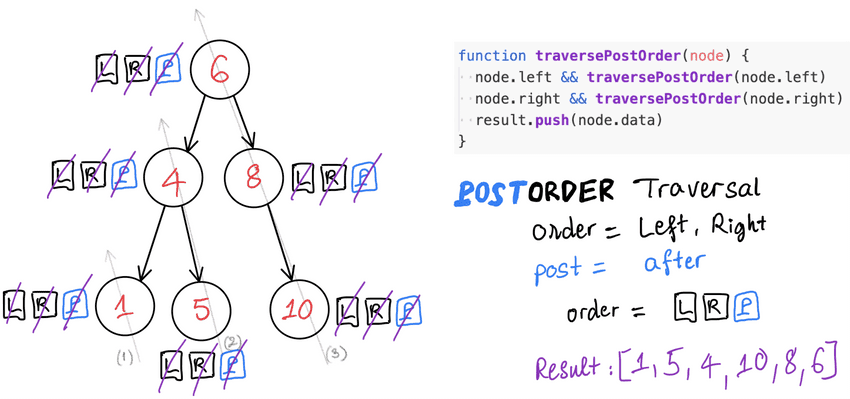
PostOrder traversal
Usefulness of this order of node visitation: whenever it gives value to your application.
// Binary Search Tree, without self-balancing
class BinarySearchTree {
// ...
// postorder traversal
postOrder() {
if (this.root == null) {
return null
} else {
var result = []
traversePostOrder(this.root)
return result
function traversePostOrder(node) {
node.left && traversePostOrder(node.left)
node.right && traversePostOrder(node.right)
result.push(node.data)
}
}
}
}$ node binary-search-tree-data-structure.js
postOrder(): [ 1, 5, 4, 10, 8, 6 ]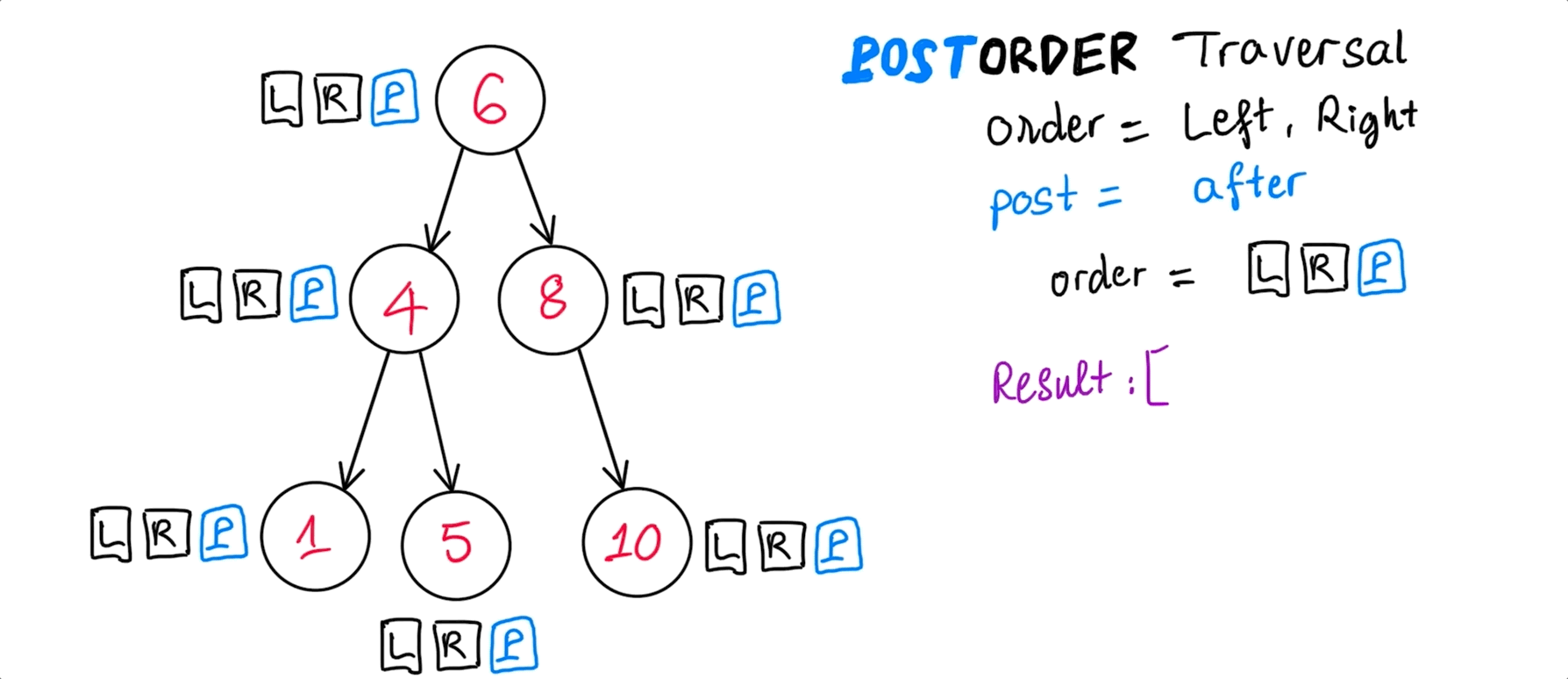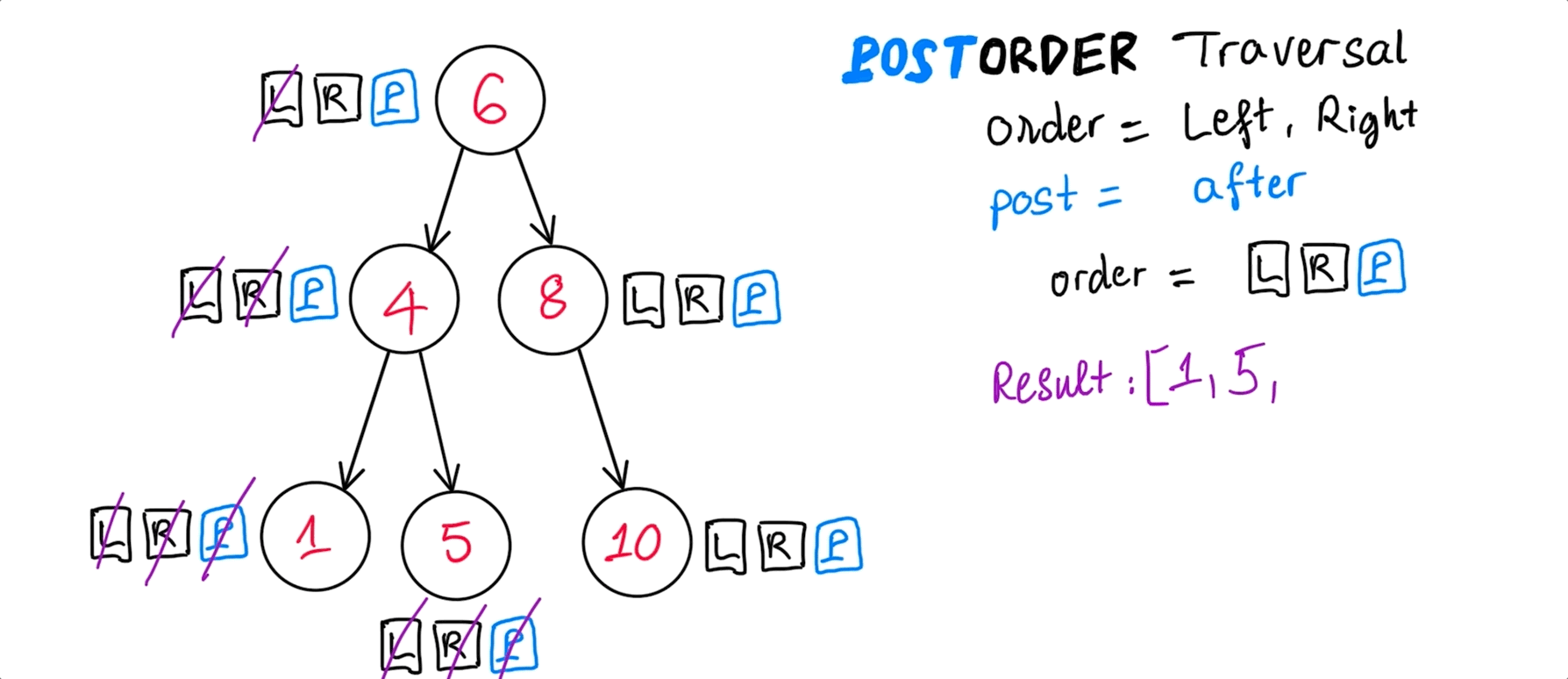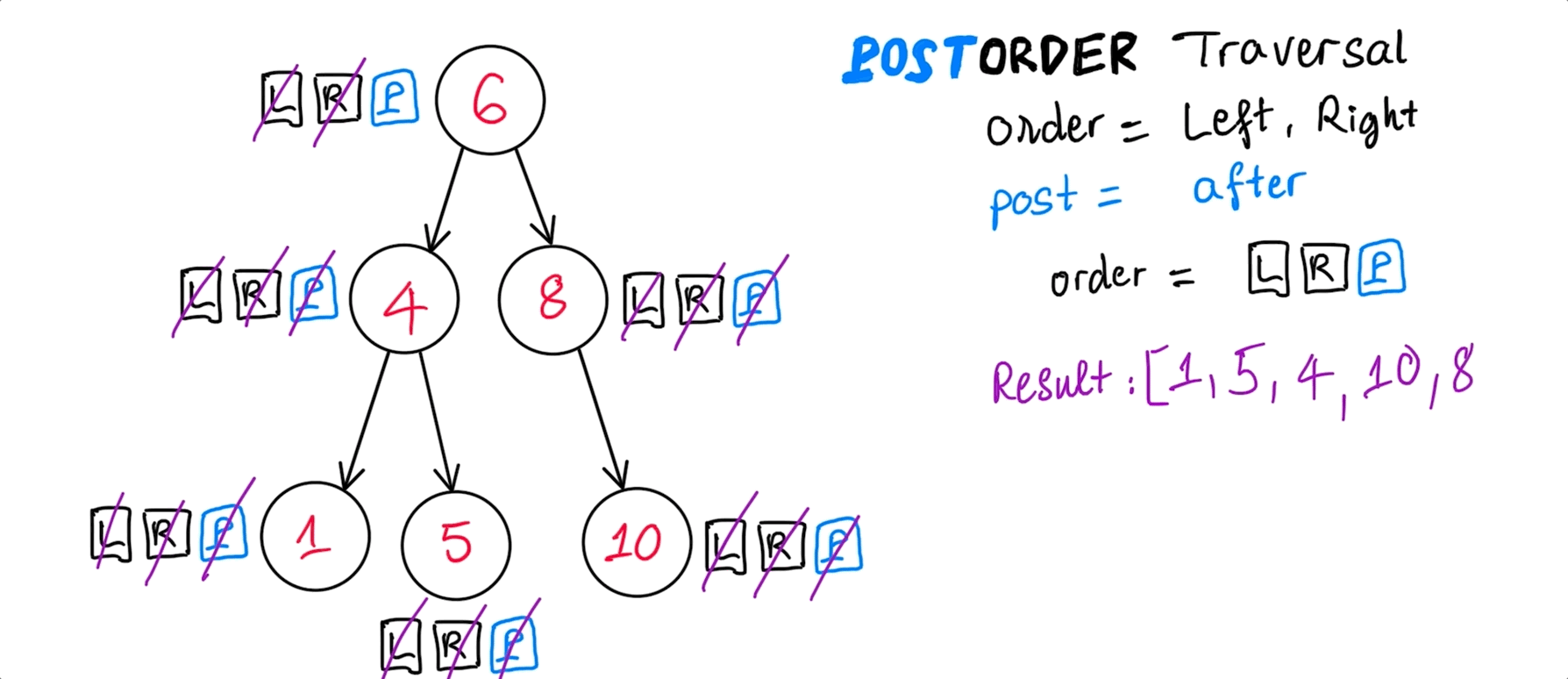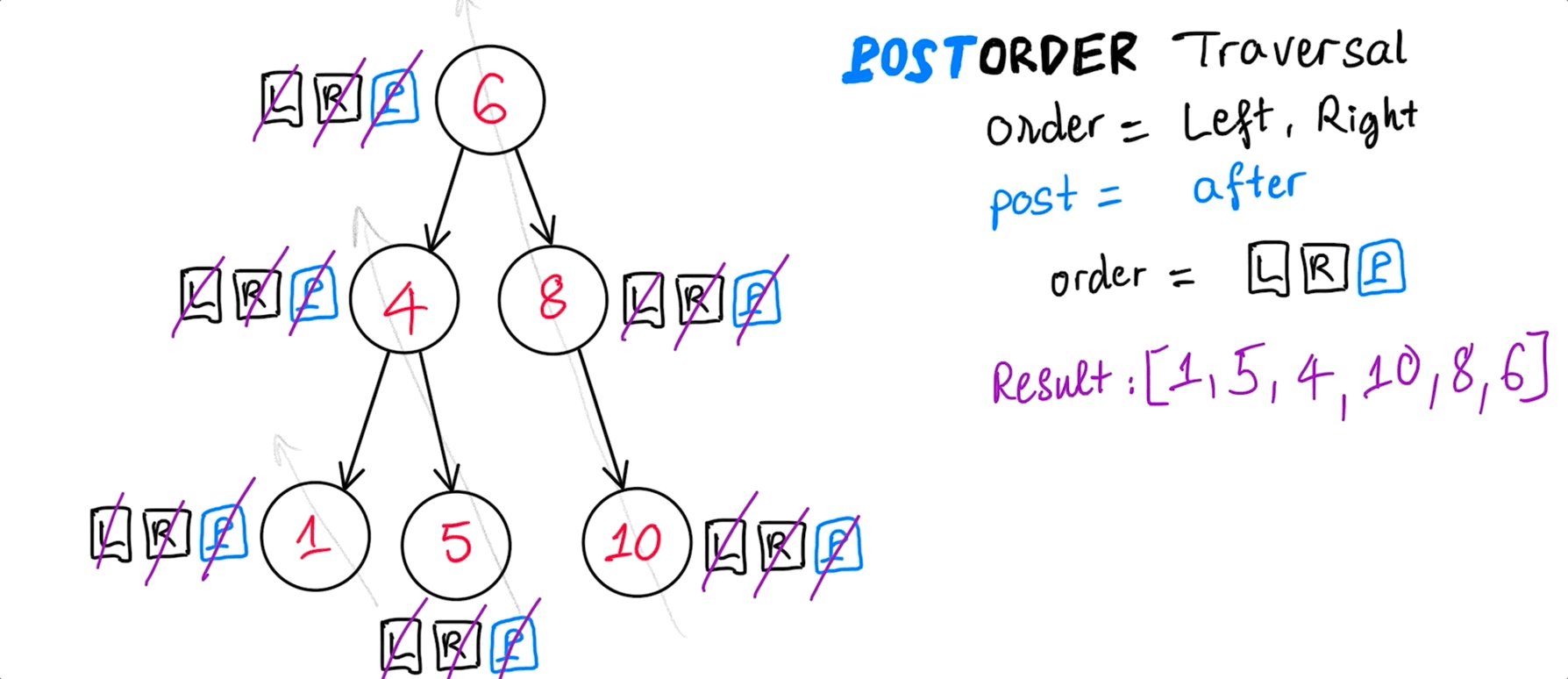
PreOrder, InOrder, PostOrder traversal summary
preorder |
inorder |
postorder |
|---|---|---|
| push, left, right | left, push, right | left, right, push |
result.push(node.data) node.left && traverse(node.left) node.right && traverse(node.right) |
node.left && traverse(node.left) result.push(node.data) node.right && traverse(node.right) |
node.left && traverse(node.left) node.right && traverse(node.right) result.push(node.data) |
| print min -> max |
3 lines of code, we have total 6 possible arrangements. 3 of them has offical names. The rest 3 doesn't. But they actually have the same usefulness. For simplicity, we can call them: prereversedorder, inreversedorder and postreversedorder. Discover them yourself!
How fast to insert/delete/access/search data
| Data Structure | Insert | Delete | Access | Search |
|---|---|---|---|---|
| Tree | O(n) | O(n) | N/A | O(n) |
| Binary Tree | O(n) | O(n) | N/A | O(n) |
Unbalanced Binary Search Tree findMin, findMax: O(n) |
O(n) | O(n) | N/A | O(n) |
| Balanced Binary Search Tree (AVL tree/Red-Black tree) findMin, findMax: O(logn) |
O(logn) | O(logn) | N/A | O(logn) |
⬆️ Time complexity (worst case) per operation
Algorithms: how to extract useful information out of input
| Common input | Problem type/human thought | Equivalent computer programming |
|---|---|---|
| Tree | Visit nodes in a particular order. | use loop/recursion to visit all nodes, use stack/queue or change position of recursive call to control the order of node visitation. |
Real life interview questions
- Draw call stack + recursion tree for
PreOrdertraversal. - Draw call stack + recursion tree for
InOrdertraversal. - Draw call stack + recursion tree for
PostOrdertraversal. - Randomly choose one of:
PreReversedOrder,InReversedOrderandPostReversedOrdertraversal, draw call stack + recursion tree for it. - Solve problem 3, 4 in popular tree problems.
- Solve Leetcode #99: Recover Binary Search Tree
- Solve Leetcode #124: Binary Tree Maximum Path Sum
- Solve Leetcode #515: Find Largest Value in Each Tree Row