Dynamic Programming part 1: the importance of Depth First Search in DP

February 25th, 2023/Share

fundamentals

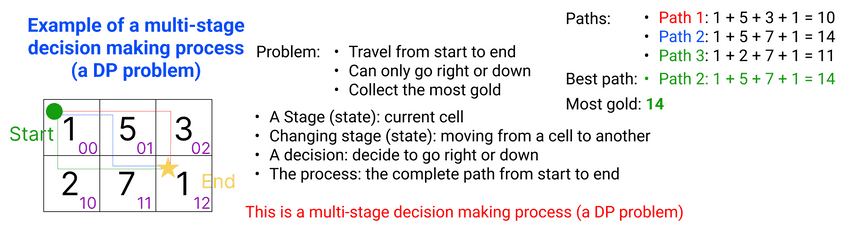
This tutorial is a part of the Data Structures and Algorithms class:

Outcomes after this Dynamic Programming (DP) series

✅ Understand what types of problem can be solved with DP
✅ Can actually apply modern DP to solve problems with 3 simple steps
✅ Can calculate the exact Time & Space complexity of a DP algorithm
✅ Clear your mind off the myths about DP related terms on the internet: principle of optimality, find subproblem, optimal substructure, bottom up, top down, tabular approach, memoization approach
✅ Use DP to solve these applications: 1. Min, 2. Max, 4. Find most optimal solution:
- Max profit/min cost/optimal choices
- Optimal sequence of actions to achieve best outcome
- Simulation: simulate different scenarios of something in life and choose the best scenario.

Prerequisites

If you knew something about DP: temporarily forget everything you've heard about DP.
DP requires a lot of previous knowledge. ONLY proceed after learning these:

Introducing The Modern Law of Dynamic Programming (Sam's DP)

Paper: The Modern Law of Dynamic Programming by Sam Tran 2023

Paper: The Theory of Dynamic Programming - Bellman 1954 - original paper

What you're going to learn is very different. It's still Dynamic Programming. But it's very different from the original DP from the original author - Richard Bellman. And it's definitely very different from anything you can find on the internet (up to the time of making of this video). But to be clear, it's a continuation of understanding and applying DP. It doesn't mean to replace anything, rather, it's a supplement for you to better understand and apply DP. It'll be clearer with the comparison table later.

The purpose stays the same: Sam's DP purpose is to helps you to pass difficult coding interviews, understand and apply DP in your daily work, life.

Summary of The Modern Law of Dynamic Programming (Sam's DP):

Sam's DP is a law, it can be proven. As opposed to Bellman's original DP, it was initially called a theory. Theory does not require proof.
The difference: law is meant to be always true (with proof). Theory can be true or false (so no proof required). That means a law guarantees a result. A theory can/can't give a result.
Mainly designed for solving coding interview purposes.
Secondly, to clear the myths about Dynamic Programming.
Thirdly, to introduce the importance of computer simulation in human's life (now and far future).

The Modern Law of Dynamic Programming (Sam's DP)

If you can describe your system as follow:

A system state: is comprised of a limited number of parameters.

Choices to change state: is a limited, known number of choices to change the system state. You have the same choices at any state.

Final states: are the states that achieve your desired information, or the states where you can't choose any choices to change system state.

Can reach final states: after a finite number of choices to change state, you can reach your final state(s).

Your system can fit in a computer in terms of RAM and CPU.

Then with Sam's DP:

You are guaranteed to have a systematic procedure to design and code your solution.

You are guaranteed to have the best answer based on your requirements (min, max, best course of actions, ...)

The Time and Space Complexity of your solution are always equal.

The Time and Space Complexity will be in polynomials (One of O(n), O(n^2), ...).

The Space Complexity equals to the number of distinct states created.

Examples:

You are the president of a nation. Your nation has money and choices to spend it. What activity do you choose to spend to make the most impact?
You are a skilled worker, working 8h/day, 9-5. There are tasks associated with time frames and reward money. Which series of tasks should you choose to maximize earning within your work schedule?

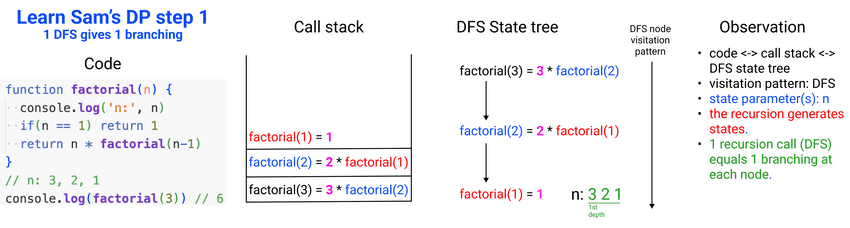
Learn Sam's DP step 1: 1 Depth First Search gives 1 branching

First we'll learn about the importance of Depth First Search in DP: it helps to generate states with predefined choices. Focus on relating the code to the call stack to the DFS state tree.

lecture-31/factorial.js

// Learn Sam's DP step 1: 1 Depth First Search gives 1 branching

function factorial(n) {
  console.log('n:', n)
  if(n == 1) return 1
  return n * factorial(n-1)
}
// n: 3, 2, 1, f(3) = 3*2*1 = 6
console.log(factorial(3)) // 6

$ node factorial.js
n: 3
n: 2
n: 1
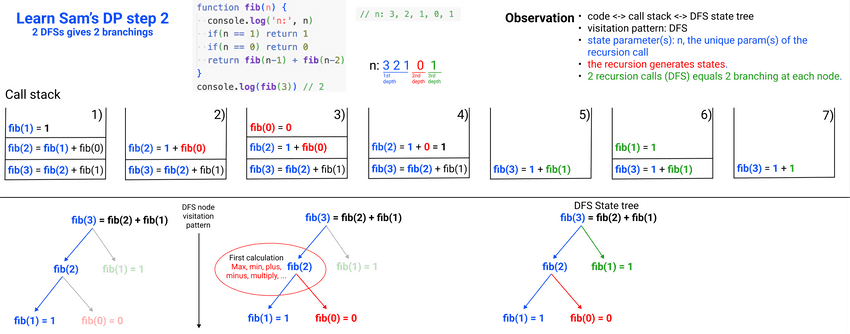
6

Learn Sam's DP step 2: 2 Depth First Searches give 2 branchings

lecture-31/fibonacci.js

// Learn Sam's DP step 2: 2 Depth First Searches give 2 branchings

function fib(n) {
  console.log('n:', n)
  if(n == 1) return 1
  if(n == 0) return 0
  return fib(n-1) + fib(n-2)
}
console.log(fib(3)) // 2
// n: 3, 2, 1, 0, 1

$ node fibonacci.js
n: 3
n: 2
n: 1
n: 0
n: 1
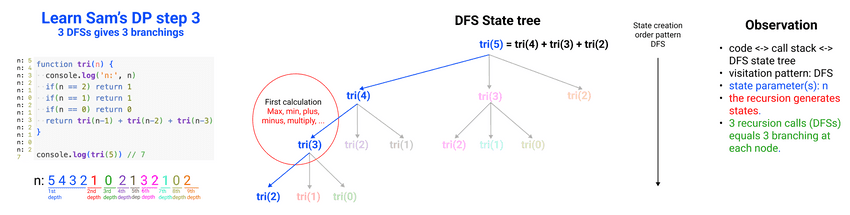
2

Learn Sam's DP step 3: 3 Depth First Searches give 3 branchings

lecture-31/tribonacci.js

// Learn Sam's DP step 3: 3 Depth First Searches give 3 branchings

function tri(n) {
  console.log('n:', n)
  if(n == 2) return 1
  if(n == 1) return 1
  if(n == 0) return 0
  return tri(n-1) + tri(n-2) + tri(n-3)
}

console.log(tri(5)) // 7

// n: 5 4 3 2 1 0 2 1 3 2 1 0 2

$ node tribonacci.js
n: 5
n: 4
n: 3
n: 2
n: 1
n: 0
n: 2
n: 1
n: 3
n: 2
n: 1
n: 0
n: 2
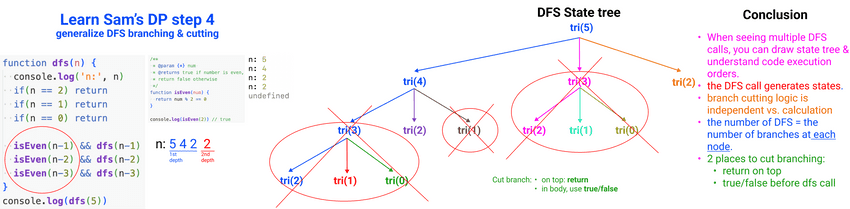
7

Learn Sam's DP step 4: generalize DFS branching & cutting

lecture-31/tribonacci-branch-cut.js

// Learn Sam's DP step 4: generalize DFS branching & cutting

function dfs(n) {
  console.log('n:', n)
  if(n == 2) return
  if(n == 1) return
  if(n == 0) return

  isEven(n-1) && dfs(n-1)
  isEven(n-2) && dfs(n-2)
  isEven(n-3) && dfs(n-3)
}
console.log(dfs(5))

// n: 5 4 2 2

/**
 * @param {*} num 
 * @returns true if number is even,
 * return false otherwise
 */
function isEven(num) {
  return num % 2 == 0
}

console.log(isEven(2)) // true

$ node tribonacci-branch-cut.js
n: 5
n: 4
n: 2
n: 2
undefined
true

Depth First Search branching & cutting summary

When seeing multiple recursive calls, you should no long be afraid. Instead you should comfortably draw state trees & understand code execution orders.
When applying this DFS branching & cutting pattern, name your recursion function DFS to emphasize the important role of DFS.
The DFS call generates states.
Branching & cutting logic is independent with calculation.
The number of DFS calls = the number of branches at each node.
There are 2 places to cut branching:
- return on top.
- true/false logic to run DFS calls within the body.
Now you can use multiple DFS calls to create/cut whatever branching you want.
Depth First Search is a subject we have learnt quite intensively. You can treat the DFS State Tree as a graph. And apply what you have learnt from with DFS to explore any kind of information you want: collecting nodes data in DFS pattern, calculate top-down or bottom-up, ...

Real life interview questions

What is the importance of DFS to DP?
Draw the mapping of a 2 choices, 3 choices call stack to DFS state tree.
Draw call stack of Tribonacci and explain why the console outputs like so.
Draw call stack of branch cut Tribonacci to check if the state print out is correct.
Remove returned value(s) & remove calculation (*, +) of factorial, fibonacci and observe if there are any changes on the state output in the console. Explain why/why not?
Use call stack to explain why the first calculation of the functions (factorial, fibonacci, ...) always happens at the last branching node on the left most branch?
Draw DFS state tree of quadonacci (4), code, print out states and draw call stack to check if your DFS state tree is correct.
Apply different calculations: min, max, plus, multiply, minus, divide, see if the tree state output on the console is different. Why/why not?
Choose a function with DFS recursive call(s) you were confused about before and apply this pattern to see if you can clearly understand what the function does now. Explain why yes/no?