*Prerequisite: The Modern Law of Dynamic Programming Part 1 & 2.
This tutorial is a part of the Data Structures and Algorithms class:
- Step 0: is it a multi-stage decision making process problem?
- Step 1: solve the problem with pen and paper, then code DFS state tree
- Step 2: calculate the information asked, bottom-up
- Step 3: cache distinct DFS calls
- Testing with Leetcode test cases
- Characteristics of problems can be solved by Sam's DP
- Let's connect and help the world to demystify Dynamic Programming
Step 0: is it a multi-stage decision making process problem?

Step 1: solve the problem with pen and paper, then code DFS state tree
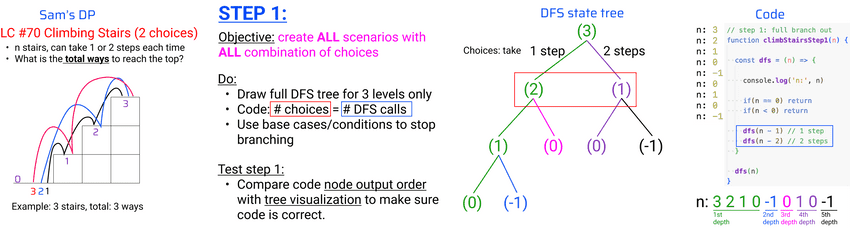
lecture-33/climbing-stairs.js
// Sam's DP, Leetcode #70: https://leetcode.com/problems/climbing-stairs/description/
// step 1: full branch out
function climbStairsStep1(n) {
const dfs = (n) => {
console.log('n:', n)
if(n == 0) return
if(n < 0) return
dfs(n - 1) // 1 step
dfs(n - 2) // 2 steps
}
dfs(n)
}$ node climbing-stairs.js
n: 3
n: 2
n: 1
n: 0
n: -1
n: 0
n: 1
n: 0
n: -1
climbStairsStep1 3: undefinedStep 2: calculate the information asked, bottom-up
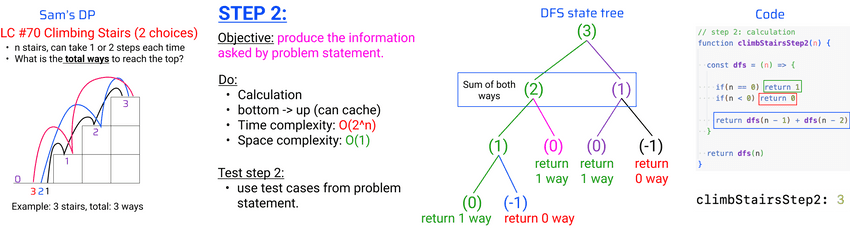
lecture-33/climbing-stairs.js
// step 2: calculation
function climbStairsStep2(n) {
const dfs = (n) => {
if(n == 0) return 1
if(n < 0) return 0
return dfs(n - 1) + dfs(n - 2)
}
return dfs(n)
}$ node climbing-stairs.js
climbStairsStep2 3: 3Step 3: cache distinct DFS calls
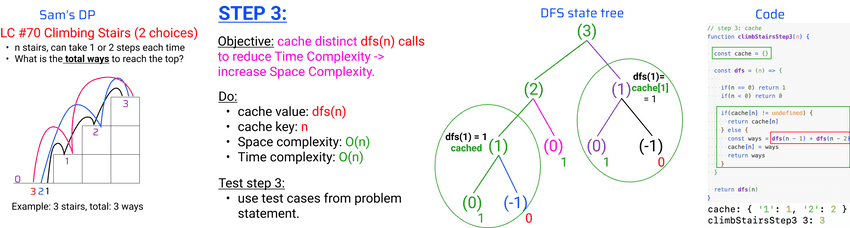
lecture-33/climbing-stairs.js
// step 3: cache
function climbStairsStep3(n) {
const cache = {}
const dfs = (n) => {
if(n == 0) return 1
if(n < 0) return 0
if(cache[n] != undefined) {
return cache[n]
} else {
// console.log('n:', n)
const ways = dfs(n - 1) + dfs(n - 2)
cache[n] = ways
return ways
}
}
return dfs(n)
}
console.log('climbStairsStep1:', climbStairsStep1(3))
console.log('climbStairsStep2:', climbStairsStep2(3)) // 3
console.log('climbStairsStep3:', climbStairsStep3(3)) // 3
// console.time('no cache')
// console.log('climbStairsStep2:', climbStairsStep2(40)) // 3
// console.timeEnd('no cache') // no cache: 2251.742ms
// console.time('cached')
// console.log('climbStairsStep3:', climbStairsStep3(40)) // 3
// console.timeEnd('cached') // cached: 0.055ms$ node climbing-stairs.js
climbStairsStep3 3: 3
climbStairsStep2 40: 165580141
no cache: 2235.300ms
climbStairsStep3 40: 165580141
cached: 0.054msTesting with Leetcode test cases
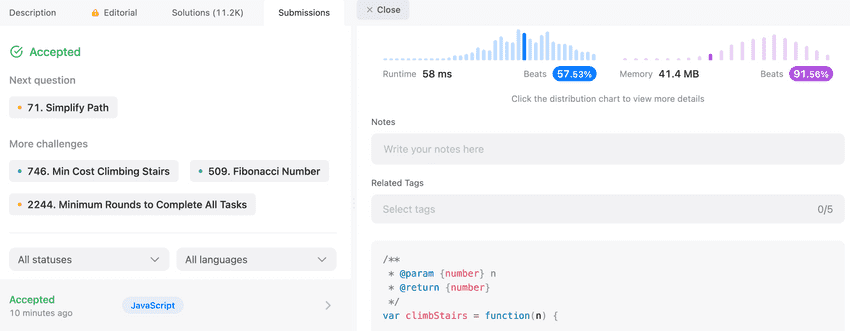
Characteristics of problems can be solved by Sam's DP
| Problem | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|
| Multi-stage decision making process (Dynamic Programming problems) | - any (array, string, graph, ...) | Sam's DP | O(states created) |
Let's connect and help the world to demystify Dynamic Programming
- I'd love to hear your learning stories as well as how my DSA course can be improved to help you learn better. Come say hi on my Linkedin!
- Dynamic Progamming is a myth with almost everyone right now. If you find this profoundly useful. Probably it'll be useful with a lot of people too. That so, let's help the world to demystify Dynamic Programming by share, like, subscribe and comment on the Youtube videos. It'll help to spread the video faster.
Real life interview questions
Type 1: a few choices
- Leetcode #509. Fibonacci Number
- Leetcode #1137. N-th Tribonacci Number
- Leetcode #70. Climbing Stairs
- Leetcode #198. House Robber
- Leetcode #213. House Robber II
- Leetcode #72. Edit Distance
- Leetcode #1547. Minimum Cost to Cut a Stick
- Leetcode #714. Best Time to Buy and Sell Stock with Transaction Fee
- Leetcode #122. Best Time to Buy and Sell Stock II
- Leetcode #123. Best Time to Buy and Sell Stock III
- Leetcode #322. Coin Change
Type 2: n choices
- Leetcode #322. Coin Change
- Leetcode #518. Coin Change II
- 0/1 Knapsack
- Leetcode #1691. Maximum Height by Stacking Cuboids
Type 3: full data point combinations