*Prerequisite: The Modern Law of Dynamic Programming Part 1 & 2.
This tutorial is a part of the Data Structures and Algorithms class:
- Step 0: is it a multi-stage decision making process problem?
- Step 1: solve the problem with pen and paper, then code DFS state tree
- Step 2: calculate the information asked, bottom-up
- Step 3: cache distinct DFS calls
- Testing with Leetcode test cases
- Characteristics of problems can be solved by Sam's DP
- Let's connect and help the world to demystify Dynamic Programming
Step 0: is it a multi-stage decision making process problem?

Step 1: solve the problem with pen and paper, then code DFS state tree
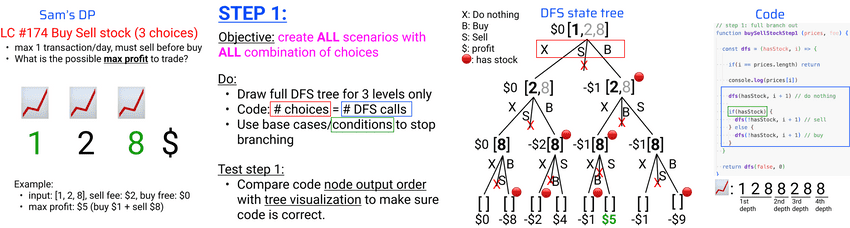
lecture-35/buy-sell-stock.js
// Sam's DP, Leetcode #714: https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/description/
// step 1: full branch out
function buySellStockStep1 (prices, fee) {
const dfs = (hasStock, i) => {
if(i == prices.length) return
console.log(prices[i])
dfs(hasStock, i + 1) // do nothing
if(hasStock) {
dfs(!hasStock, i + 1) // sell
} else {
dfs(!hasStock, i + 1) // buy
}
}
return dfs(false, 0)
}$ node buy-sell-stock.js
1
2
8
8
2
8
8
buySellStockStep1: undefinedStep 2: calculate the information asked, bottom-up
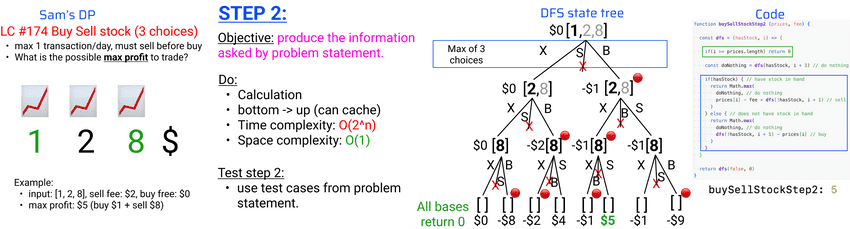
lecture-35/buy-sell-stock.js
// step 2: calculation
function buySellStockStep2 (prices, fee) {
const dfs = (hasStock, i) => {
if(i >= prices.length) return 0
const doNothing = dfs(hasStock, i + 1) // do nothing
if(hasStock) { // have stock in hand
return Math.max(
doNothing, // do nothing
prices[i] - fee + dfs(!hasStock, i + 1) // sell
)
} else { // does not have stock in hand
return Math.max(
doNothing, // do nothing
dfs(!hasStock, i + 1) - prices[i] // buy
)
}
}
return dfs(false, 0)
}$ node buy-sell-stock.js
buySellStockStep2: 5Step 3: cache distinct DFS calls
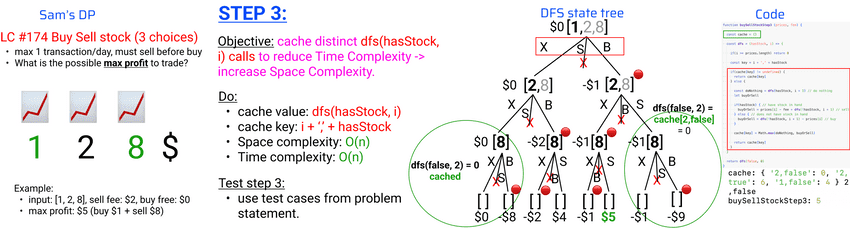
lecture-35/buy-sell-stock.js
// step 3: cache
function buySellStockStep3 (prices, fee) {
const cache = {}
const dfs = (hasStock, i) => {
if(i >= prices.length) return 0
const key = i + ',' + hasStock
if(cache[key] != undefined) {
return cache[key]
} else {
const doNothing = dfs(hasStock, i + 1) // do nothing
let buyOrSell
if(hasStock) { // have stock in hand
buyOrSell = prices[i] - fee + dfs(!hasStock, i + 1) // sell
} else { // does not have stock in hand
buyOrSell = dfs(!hasStock, i + 1) - prices[i] // buy
}
cache[key] = Math.max(doNothing, buyOrSell)
return cache[key]
}
}
return dfs(false, 0)
}
console.log('buySellStockStep1:', buySellStockStep1([1,2,8], 2))
console.log('buySellStockStep2:', buySellStockStep2([1,2,8], 2))
console.log('buySellStockStep3:', buySellStockStep3([1,2,8], 2))
// console.time('no cache')
// console.log(buySellStockStep2([1036,2413,2776,825,2640,31,1560,2917,4282,783,3146,2600,1939,694,4284,3881,554,167,372,4620,3037,1175,1075,3845,4981,4495,3406], 655)) // 17533
// console.timeEnd('no cache') // no cache: 1962.271ms
// console.time('cached')
// console.log(buySellStockStep3([1036,2413,2776,825,2640,31,1560,2917,4282,783,3146,2600,1939,694,4284,3881,554,167,372,4620,3037,1175,1075,3845,4981,4495,3406], 655)) // 17533
// console.timeEnd('cached') // cached: 0.130ms$ node buy-sell-stock.js
buySellStockStep3: 5
17533
no cache: 1839.498ms
17533
cached: 0.135msTesting with Leetcode test cases
Characteristics of problems can be solved by Sam's DP
| Problem | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|
| Multi-stage decision making process (Dynamic Programming problems) | - any (array, string, graph, ...) | Sam's DP | O(states created) |
Let's connect and help the world to demystify Dynamic Programming
- I'd love to hear your learning stories as well as how my DSA course can be improved to help you learn better. Come say hi on my Linkedin!
- Dynamic Progamming is a myth with almost everyone right now. If you find this profoundly useful. Probably it'll be useful with a lot of people too. That so, let's help the world to demystify Dynamic Programming by share, like, subscribe and comment on the Youtube videos. It'll help to spread the video faster.
Real life interview questions
Type 1: a few choices
- Leetcode #509. Fibonacci Number
- Leetcode #1137. N-th Tribonacci Number
- Leetcode #70. Climbing Stairs
- Leetcode #198. House Robber
- Leetcode #213. House Robber II
- Leetcode #72. Edit Distance
- Leetcode #1547. Minimum Cost to Cut a Stick
- Leetcode #714. Best Time to Buy and Sell Stock with Transaction Fee
- Leetcode #122. Best Time to Buy and Sell Stock II
- Leetcode #123. Best Time to Buy and Sell Stock III
- Leetcode #322. Coin Change
Type 2: n choices
- Leetcode #322. Coin Change
- Leetcode #518. Coin Change II
- 0/1 Knapsack
- Leetcode #1691. Maximum Height by Stacking Cuboids
Type 3: full data point combinations
