Graph Data Structure

/
fundamentals

This tutorial is a part of the Data Structures and Algorithms class:

Why do we need graph

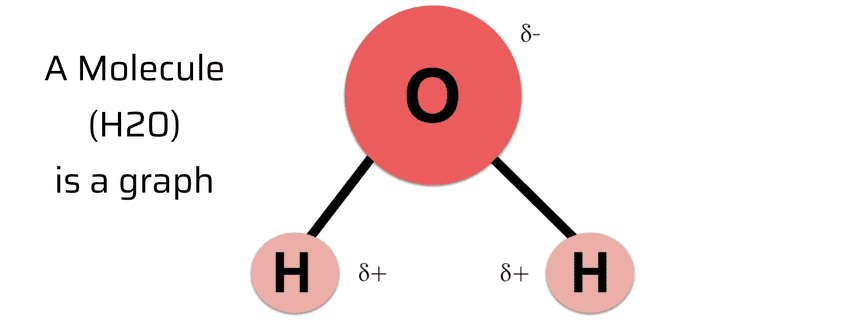
  • Graph is a data structure used to model relationships between entities. Tree is a graph.
  • Graph is an extremely popular data structure because anything has relationship.
  • We'll learn to: present a graph into code and draw a visual graph from code.
  • 2 popular ways to present graph: adjacency list and adjacency matrix.

h2o molecule

Directed, unweighted graph: visual graph <=> code

directed unweighted graph

  • Adjacency list: list of immediate neighbors.
  • Adjacency matrix: nxn matrix (n nodes) of immediate neighbors.
  • List is dense. Matrix is sparse.
  • Navigate around graph both with: visual graph <=> code (1 to 1 mapping).
  • Graph most important problem: is there a possible path from one node to another?

Directed, weighted graph: visual graph <=> code

directed weighted graph

Some graph problems in real life:

  • Find all possible routes from SFO to JFK.
  • Find cheapest flight from SFO to JFK.
  • Find shortest flight from SFO to JFK.

Undirected, unweighted graph: visual graph <=> code

undirected unweighted graph

Undirected, weighted graph: visual graph <=> code

undirected weighted graph

Graph problems and algorithms

  • Problems:

    • 1. Visit (collect data) nodes in a particular order. Ex: how to go from SFO -> IAH? Option 1: SFO -> ORD -> JFK -> IAH. Do Jack & Jill have shared friends?
    • 2. Modify graph to satisfy some conditions. Ex: what's the minimum bridges should we remove to isolate 2 connected cities?

  • Algorithms:

    • Human has been conducting extensive researches on graph algorithms.
    • We will discuss in details some most frequently used ones in coming dedicated tutorials.

  • Key take away from today:

    • How to present graph <=> code.
    • How to navigate from node to node by looking at the code.

  • Optional challenge:

Real life interview questions

  1. Translate all visual graphs above into code by yourself.
  2. Translate all code presentations above into visual graph by yourself.
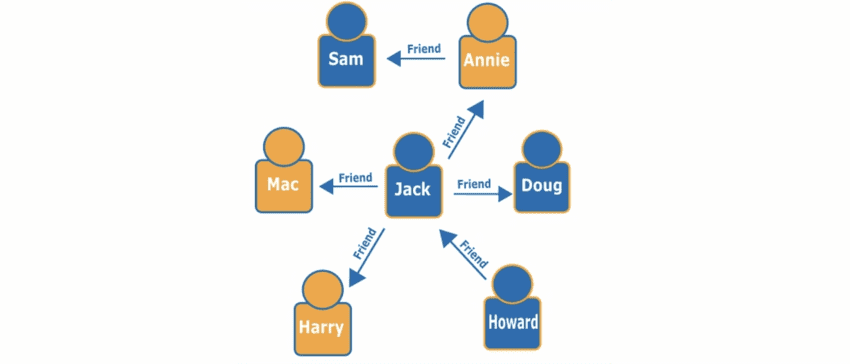
  3. Present this simple social network graph in code using both adjacency list and matrix. Write simple, separate programs (for both list + matrix presentations) to print out all the friends a person has. Ex: Friend(s) of Howard: Jack.

social network graph

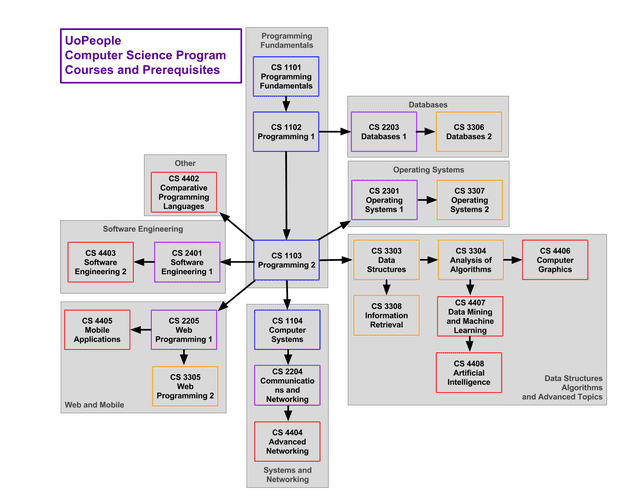
  1. Present this class prerequisites relationship in code using both adjacency list and matrix. Looking at the list and matrix, just by rough counting, estimate how much space does list need compared with matrix in percentage. (For example, list only take 10% of space compared to matrix).

classes prerequisites

  1. For the list and matrices in problem 3 and 4. If you don't carefully document your code, can anyone (or even future you) read and interprete the code into a different visual graph than the original graph? Why/why not? What options can you think of to prevent this error?
  2. For all the ajacency list presentations of the graphs you have above, just by looking at them, transform them into ajacency matrix.
  3. For all the ajacency matrix presentations of the graphs you have above, just by looking at them, transform them into ajacency list.
  4. Optional problems: solve airport problems mentioned above.