*Prerequisite: Tree data structure part 2/5: balanced/unbalanced Binary Search Tree.
This tutorial is a part of the Data Structures and Algorithms class:
- Extracting useful information out of trees
- Difference of Human vs. Computer when solving problems
- While to see all nodes, Queue to control the order of visit
- While to see all nodes, Stack to control the order of visit
Extracting useful information out of trees
Motivations from real life applications and coding interview questions:
... endless number of questions, is there a simple way to solve these questions? The short answer is yes, there's one pattern to solve them (all). It turns out to answer (most of) these questions, we need to visit all nodes + change the order of visiting according to required logic. So:
- To visit all nodes: use loop (for, while, ...) or recursion.
-
To control the order of which node to visit first:
- for loop: use (single/multiple) Stack/Queue or a combination of both.
- for recursion: change the position of the recursion call.
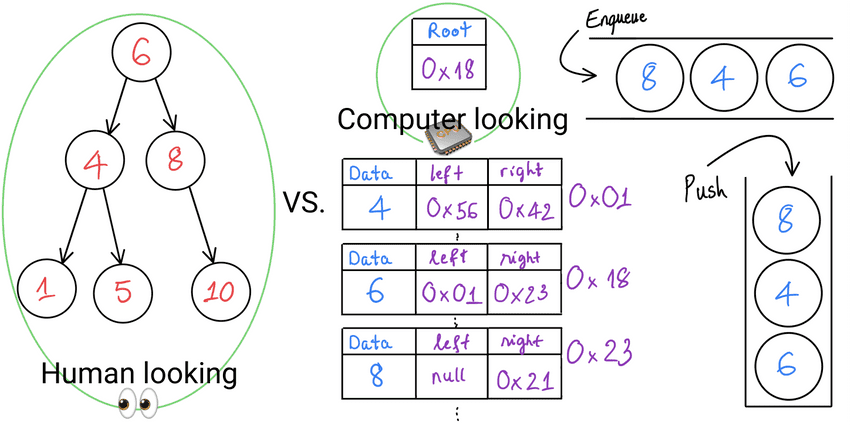
Difference of Human vs. Computer when solving problems
| Human thought | Human action | Equivalent computer execution |
|---|---|---|
| looking at data | see the whole tree at a time | look at one node at a time + apply logic to only current node + use loop/recursion to visit all nodes |
| node selection | freely select nodes as asked | use Stack or Queue or change position of recursive call to control the order of node selection |
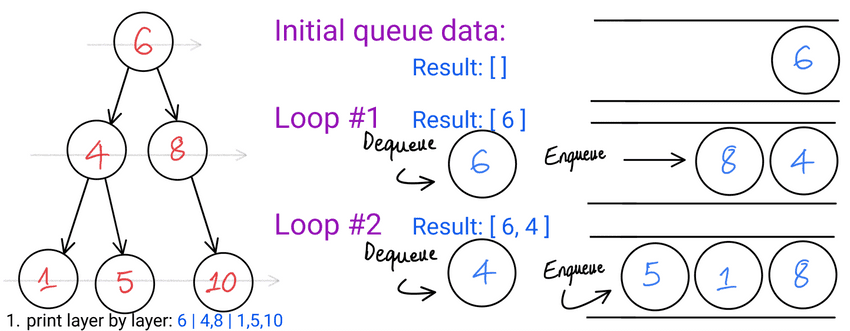
While to see all nodes, Queue to control the order of visit
Queue allows us to visit nodes layer by layer, closest layer first (Breadth First Search).
lecture-11/while-loop-and-queue.js
// structure of a node
class Node {
constructor(data) {
this.data = data
this.left = null
this.right = null
}
}
// Binary Tree
class BinaryTree {
constructor(data) {
this.root = data ? new Node(data) : null
}
}
// create new binary tree
const binaryTree = new BinaryTree(6)
binaryTree.root.left = new Node(4)
binaryTree.root.left.left = new Node(1)
binaryTree.root.left.right = new Node(5)
binaryTree.root.right = new Node(8)
binaryTree.root.right.right = new Node(10)
console.log(JSON.stringify(binaryTree, null, 4))
const traverseWithWhileAndQueue = (root) => { // aka Breadth First Search
const queue = [root]
const result = []
let loopCount = 1
console.log('initial queue data: ', queue[0].data)
while(queue.length > 0) {
console.log('loop #:', loopCount)
loopCount++
const queueData = queue.map(e => e.data )
console.log('queue data: ', queueData)
const currentNode = queue.shift() // dequeue
currentNode.left && queue.push(currentNode.left) // enqueue
currentNode.right && queue.push(currentNode.right) // enqueue
result.push(currentNode.data) // process current node data
console.log('result: ', result)
console.log('- - - - - - - - -')
}
}
traverseWithWhileAndQueue(binaryTree.root)$ node while-loop-and-queue.js
{
"root": {
"data": 6,
"left": {
"data": 4,
"left": {
"data": 1,
"left": null,
"right": null
},
"right": {
"data": 5,
"left": null,
"right": null
}
},
"right": {
"data": 8,
"left": null,
"right": {
"data": 10,
"left": null,
"right": null
}
}
}
}
initial queue data: 6
loop #: 1
queue data: [ 6 ]
result: [ 6 ]
- - - - - - - - -
loop #: 2
queue data: [ 4, 8 ]
result: [ 6, 4 ]
- - - - - - - - -
loop #: 3
queue data: [ 8, 1, 5 ]
result: [ 6, 4, 8 ]
- - - - - - - - -
loop #: 4
queue data: [ 1, 5, 10 ]
result: [ 6, 4, 8, 1 ]
- - - - - - - - -
loop #: 5
queue data: [ 5, 10 ]
result: [ 6, 4, 8, 1, 5 ]
- - - - - - - - -
loop #: 6
queue data: [ 10 ]
result: [ 6, 4, 8, 1, 5, 10 ]
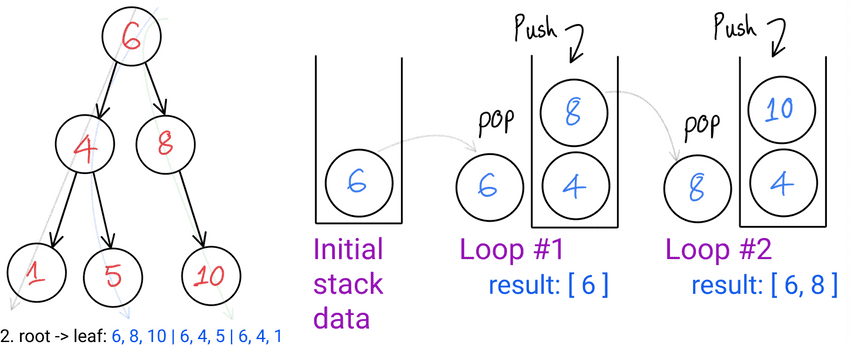
- - - - - - - - -While to see all nodes, Stack to control the order of visit
Stack allows us to visit nodes from root to leaf first (Depth First Search).
lecture-11/while-loop-and-stack.js
// structure of a node
class Node {
constructor(data) {
this.data = data
this.left = null
this.right = null
}
}
// Binary Tree
class BinaryTree {
constructor(data) {
this.root = data ? new Node(data) : null
}
// search if data is in binary search tree, return node/false
search(data) {
let current = this.root
while(current) {
if(current.data === data) {
return current
} else if(current.data > data) {
current = current.left
} else {
current = current.right
}
}
return false
}
}
// create new binary tree
const binaryTree = new BinaryTree(6)
binaryTree.root.left = new Node(4)
binaryTree.root.left.left = new Node(1)
binaryTree.root.left.right = new Node(5)
binaryTree.root.right = new Node(8)
binaryTree.root.right.right = new Node(10)
console.log(JSON.stringify(binaryTree, null, 4))
const traverseWithWhileAndStack = (root) => { // aka Depth First Search
const stack = [root]
const path = []
const result = []
const visitedNodes = new Set()
let loopCount = 1
console.log('initial stack data: ', stack[0].data)
while(stack.length > 0) {
console.log('loop #:', loopCount)
loopCount++
const stackData = stack.map(e => e.data )
console.log('stack data: ', stackData)
const currentNode = stack.pop()
visitedNodes.add(currentNode.data)
currentNode.left && stack.push(currentNode.left)
currentNode.right && stack.push(currentNode.right)
path.push(currentNode.data)
// if node is a leaf, save a complete root -> leaf path
// and remove leaf from `path` variable to make way for new path
if(!currentNode.left && !currentNode.right) {
console.log('reached a leaf, path:', path)
result.push(JSON.parse(JSON.stringify(path)))
path.pop()
// if node is a parent node and both left + right child
// have been visited, remove node from `path` variable
// to make way for new path
const parentNode = binaryTree.search(path[path.length - 1])
if(parentNode) {
const leftChildVisited =
!(parentNode.left && !visitedNodes.has(parentNode.left.data))
const rightChildVisited =
!(parentNode.right && !visitedNodes.has(parentNode.right.data))
if(leftChildVisited && rightChildVisited) {
console.log('popped a parent node:', path.pop())
}
}
} else {
console.log('current path:', path)
}
if(path.length && path[path.length - 1])
console.log('- - - - - - - - -')
}
console.log('result: ', result)
}
traverseWithWhileAndStack(binaryTree.root)$ node while-loop-and-stack.js
{
"root": {
"data": 6,
"left": {
"data": 4,
"left": {
"data": 1,
"left": null,
"right": null
},
"right": {
"data": 5,
"left": null,
"right": null
}
},
"right": {
"data": 8,
"left": null,
"right": {
"data": 10,
"left": null,
"right": null
}
}
}
}
initial stack data: 6
loop #: 1
stack data: [ 6 ]
current path: [ 6 ]
- - - - - - - - -
loop #: 2
stack data: [ 4, 8 ]
current path: [ 6, 8 ]
- - - - - - - - -
loop #: 3
stack data: [ 4, 10 ]
reached a leaf, path: [ 6, 8, 10 ]
popped a parent node: 8
- - - - - - - - -
loop #: 4
stack data: [ 4 ]
current path: [ 6, 4 ]
- - - - - - - - -
loop #: 5
stack data: [ 1, 5 ]
reached a leaf, path: [ 6, 4, 5 ]
- - - - - - - - -
loop #: 6
stack data: [ 1 ]
reached a leaf, path: [ 6, 4, 1 ]
popped a parent node: 4
- - - - - - - - -
result: [ [ 6, 8, 10 ], [ 6, 4, 5 ], [ 6, 4, 1 ] ]Real life interview questions
- What's the key difference between a human and a computer when solving a tree problem? From your own opinion, what's the main reason for this difference?
- Solve problem 1, 2, 5, 6, 7 in 7 popular tree problems.
- Solution for stack example will not work in case tree height is greater than 2. Add your modification to the solution so it will work with tree with any height.
- Which/which combination/how many of Stack(s) or Queue(s) did you use to solve the problems above? Can you think of any other data structures to replace Stack or Queue to solve the same problems?