Backtracking

/
fundamentals

This tutorial is a part of the Data Structures and Algorithms class:

Part 1 (14:04):

Part 2 (11:30):

Typical problems solved by Backtracking - virtually any problem

  • Backtracking is a "smart" brute-force solution, uses DFS to branch out all possible solutions and Bounding conditions to stop the unnecessary branching for better performance.
  • Backtracking = DFS + Bounding conditions.
  • This is the true power of the computer for solving problems. Because in real life, there are so many problems that can't be solved logically. So we use computer to list out all choices and we choose the ones that satisfy our requirements.
  • Huge mindset switch: from solving the problems -> providing a way to list all possible cases.

backtrack n queens state tree dfs

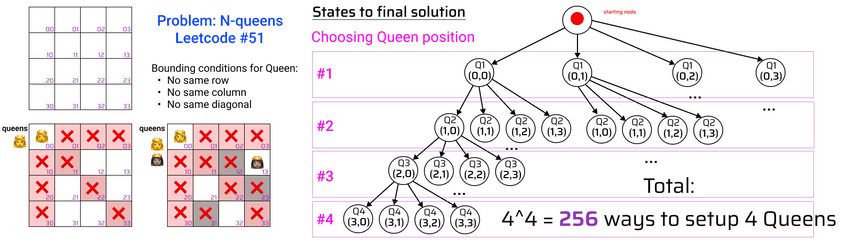
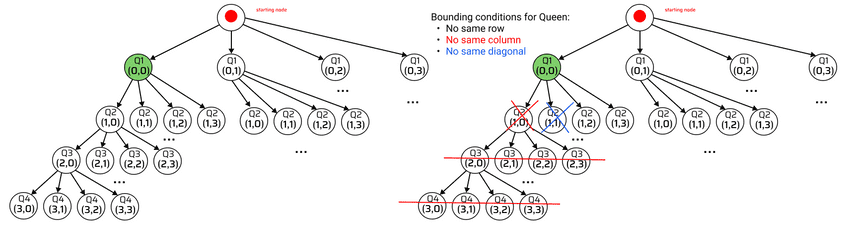
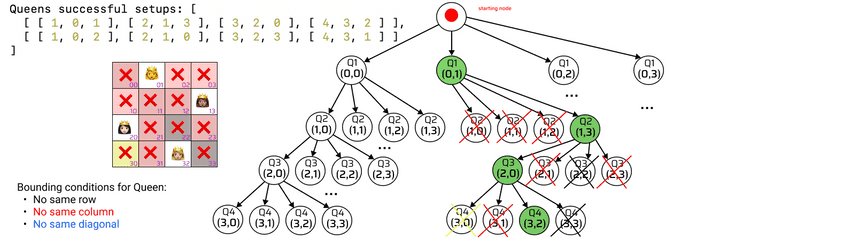
Iterative implementation of Backtracking

backtrack n queens successful setup

lecture-30/backtracking-n-queens-iterative.js
// backtracking iterative implementation - 4 queens

const backtrack4QueensIter = () => {

  const result = []
  
  for (let i = 0; i < 4; i++) {
    for (let j = 0; j < 4; j++) {
      const state2 = [
        [1, 0, i], // [queenNum, row, col] aka [queen 1, row 0, col i]
        [2, 1, j],
      ]
      if (isBound(state2)) continue

      for (let k = 0; k < 4; k++) {
        const state3 = [
          [1, 0, i],
          [2, 1, j],
          [3, 2, k],
        ]
        if (isBound(state3)) continue
        for (let l = 0; l < 4; l++) {
          const state4 = [
            [1, 0, i],
            [2, 1, j],
            [3, 2, k],
            [4, 3, l],
          ]
          if (isBound(state4)) continue
          result.push(state4)
        }
      }
    }
  }

  return result
}

console.log('Queens successful setups:', backtrack4QueensIter())


/**
 * 
 * @param {*} tempRes [ [ 1, 0, 1 ], [ 2, 1, 2 ] ]
 * @returns true | false
 */
function isBound (tempRes) {

    ////////// STEP 2: KILL the branch with BOUNDING conditions
    // STEP 2.a: prepare the bounding conditions
    const cols = new Set()
    const forbiddenPos = new Set()

    for (let j = 0; j < tempRes.length; j++) {

      let row = tempRes[j][1] + 0 // deep copy
      let col = tempRes[j][2] + 0 // deep copy
      cols.add(col) // list of cols idx of all queens

      // // forbidden next queen diag postions
      for (let k = 0; k <= 4; k++) {
        forbiddenPos.add('' + (row + 1 + k) + (col + 1 + k))
        forbiddenPos.add('' + (row - 1 - k) + (col - 1 - k))
        forbiddenPos.add('' + (row + 1 + k) + (col - 1 - k))
        forbiddenPos.add('' + (row - 1 - k) + (col + 1 + k))
      }
    }

    // get most recent queen added
    const [lqNum, lqRow, lqCol] = tempRes[tempRes.length - 1] || []

    // STEP 2.b: apply bounding condition to kill this branch if
    if (
      forbiddenPos.has('' + lqRow + lqCol) || // queen same diag
      (cols.size !== tempRes.length) // queen same col
    ) {
      console.log('Killing this branch: ', lqNum, lqRow, lqCol)
      return true // stop branching
    }
    return false // continue to branch
    ////////// STEP 2: KILL the branch with BOUNDING conditions done
}

// test bounding function
// console.log(isBound([ [ 1, 0, 1 ], [ 2, 1, 2 ] ]))
$ node backtracking-n-queens-iterative.js
Killing this branch:  2 1 0
Killing this branch:  2 1 1
...
Killing this branch:  2 1 2
Killing this branch:  2 1 3
Queens successful setups: [
  [ [ 1, 0, 1 ], [ 2, 1, 3 ], [ 3, 2, 0 ], [ 4, 3, 2 ] ],
  [ [ 1, 0, 2 ], [ 2, 1, 0 ], [ 3, 2, 3 ], [ 4, 3, 1 ] ]
]

Recursive implementation of Backtracking

backtrack n queens successful setup

lecture-30/backtracking-n-queens-recursive.js
// backtracking n queens recursive implementation

const backtrackNQueens = (n) => {

  const result = []
  const tempRes = []
  // tempRes [ [ 1, 0, 3 ], [ 2, 1, 3 ], [ 3, 2, 3 ], [ 4, 3, 3 ] ]
  // [ 1, 0, 3 ] -> [queenNum, queenRow, queenCol]

  const dfs = (queenNum, tempRes) => {

    ////////// STEP 2: KILL the branch with BOUNDING conditions

    // STEP 2.a: prepare the bounding conditions
    const cols = new Set()
    const forbiddenPos = new Set()

    for (let j = 0; j < tempRes.length; j++) {

      let row = tempRes[j][1] + 0
      let col = tempRes[j][2] + 0

      cols.add(col) // list of cols idx of all queens

      // // forbidden next queen diag postions
      for (let k = 0; k <= n; k++) {
        forbiddenPos.add('' + (row + 1 + k) + (col + 1 + k))
        forbiddenPos.add('' + (row - 1 - k) + (col - 1 - k))
        forbiddenPos.add('' + (row + 1 + k) + (col - 1 - k))
        forbiddenPos.add('' + (row - 1 - k) + (col + 1 + k))
      }
    }

    // get most recent queen added
    const [lqNum, lqRow, lqCol] = tempRes[tempRes.length - 1] || []

    // console.log('latestQ: ', lqNum, lqRow, lqCol)

    // STEP 2.b: apply bounding condition to kill this branch if
    if (
      forbiddenPos.has('' + lqRow + lqCol) || // queen same diag
      (cols.size !== tempRes.length) // queen same col
    ) {
      console.log('Killing this branch: ', lqNum, lqRow, lqCol)
      return // return to stop branching
    }
    ////////// STEP 2: KILL the branch with BOUNDING conditions done





    // console.log('tempRes: ', tempRes)
    // console.log('forbiddenPos: ', forbiddenPos)



    ////////// STEP 1: FULL branch out
    if(queenNum > n) {
      result.push([...tempRes]) // MUST push a deep copy
      // console.log('result: ', result)
      return
    }
    
    for (let i = 0; i < n; i++) {
      const qPos = [queenNum, queenNum - 1, i] // [queenNum, row, col]
      tempRes.push(qPos)
      dfs(++queenNum, tempRes)
      tempRes.pop()
      queenNum--
    }
    ////////// STEP 1: FULL branch out done
  }

  dfs(1, tempRes)


  return result
}

console.log('Queens successful setups:',  backtrackNQueens(4))
$ node backtracking-n-queens-recursive.js
Killing this branch:  2 1 0
Killing this branch:  2 1 1
...
Killing this branch:  2 1 2
Killing this branch:  2 1 3
Queens successful setups: [
  [ [ 1, 0, 1 ], [ 2, 1, 3 ], [ 3, 2, 0 ], [ 4, 3, 2 ] ],
  [ [ 1, 0, 2 ], [ 2, 1, 0 ], [ 3, 2, 3 ], [ 4, 3, 1 ] ]
]

Characteristics of problems can be solved by Backtracking

Backtracking is a powerful and simple algorithm to solve problems. It's so simple, it only has 2 steps:

  • Step 1: Use DFS to branch out and build all possible outcomes.
  • Step 2: Use Bounding conditions to remove unmeaningful banching.

Typical problems (virtually any problems because it's a "smart" brute-force):

  • Sequencial decision-making problems.
  • Problems that logical thinking creates so many choices. And trial-then-choose is more suitable.
  • Step by step (so we can branch with DFS) solution building problems.
lecture-30/backtracking-iterative.js
// Backtracking ITERATIVE implementation

// STEP 1: list all possible options, (nested FOR LOOP is DFS)
const backtrackingIterative = () => {
  for (let i = 0; i < array1.length; i++) {
    const state1 = [ ... ] // state 1 data from from array1
    for (let j = 0; j < array2.length; j++) {
      const state2 = [ ... ] // state 1 data from from array1 + array2
      for (let k = 0; index < array3.length; k++) {
        const state3 = [ ... ] // state 1 data from from array1 + array2 + array3
        ...
      }
    }
  }
}


// STEP 2: create the bounding function
function boundingFunc(state) {
  if(state) {
    ...
    return true // to stop branching
  } else {
    ...
    return false // to continue to branch
  }
}

// STEP 3: put bounding function in each state creation
const backtrackingIterative = () => {

  const result = []

  for (let i = 0; i < array1.length; i++) {
    const state1 = [ ... ] // state 1 data from from array1
    boundingFunc(state1) continue
    for (let j = 0; j < array2.length; j++) {
      const state2 = [ ... ] // state 1 data from from array1 + array2
      boundingFunc(state2) continue
      for (let k = 0; index < array3.length; k++) {
        const state3 = [ ... ] // state 1 data from from array1 + array2 + array3
        boundingFunc(state3) continue
        result.push(state3) // only final states passing one boudning condition is collected
      }
    }
  }
}
lecture-30/backtracking-recursive.js
// Backtracking RECURSIVE implementation

const backtrackingRecursive = () => {
  const result = []
  const tempRes = []

  const dfs = (tempRes) => {

    // STEP 2: apply bounding conditions to stop unmeaningful branching
    if(tempRes) {
      return // stop branching
    }
    // otherwise, let the recursive runs



    // STEP 1: dfs to collect all possible outcomes
    if(queenNum > n) {
      result.push([...tempRes]) // MUST push a deep copy
      // console.log('result: ', result)
      return
    }
    
    for (let i = 0; i < n; i++) {
      const qPos = [queenNum, queenNum - 1, i] // [queenNum, row, col]
      tempRes.push(qPos)
      dfs(++queenNum, tempRes)
      tempRes.pop()
      queenNum--
    }
  }

  dfs(...)
  return result
}

Summary

Prob. class P. sub-class Input characteristics Algorithm Time
Complexity
(almost) ANY problem class array, matrix, ... Brute Force O(n) & up
- any Backtracking Varies
- pass split test
- array, string or graph, ...
- divide, solve, combine gives a possible solution		 Divide and Conquer O(nlogn)
- accessing 2 data points at a time is useful
- closing in the pointers proven to give a correct answer
- usually array or string		 Two Pointers O(n)
1. Maximization
2. Minimization		 array, string or graph, ... Greedy choice,
no guarantee for most optimal solution		 varies
- graph or present problem with graph Bellman-Ford O(E*V)
- any Backtracking Varies
3. Find all options array, matrix, ... Brute Force O(n) & up
- any Backtracking Varies
4. Find most optimal solution - shortest/longest path
- Min/max		 - graph or present problem with graph Bellman-Ford O(E*V)
- any Backtracking Varies
5. Find a truth search for a number - sorted array
or balanced BST		 Binary Search O(logn)
accessing a few consecutive data points at the same time is necessary/useful - usually array or string Slding Window O(n)
- shortest path, equal edge weight
- node visitation layer by layer		 - graph or matrix Breadth First Search O(n)
- think top down, think bottom up
- node visitation go full depth first		 - graph or matrix Depth First Search O(n)
- what must be done first? - graph or present problem with graph Topological Sort O(n)
- shortest/longest path - graph or present problem with graph Bellman-Ford O(E*V)

Real life interview questions

  1. How does Backtracking solve problems?
  2. What kind of problems can typically be solved by Backtracking?
  3. Recalculate the Complexity of the problems above.
  4. Redo the problems above. You should be able to quickly explain how the algorithm works and implement each of them within 15 mins.
  5. What are the steps to apply Backtracking?
  6. (Medium) Leetcode #77. Combinations
  7. (Medium) Leetcode #46. Permutations
  8. (Medium) Leetcode #47. Permutations II
  9. (Medium) Leetcode #78. Subsets
  10. (Medium) Leetcode #90. Subsets II
  11. (Medium) Leetcode #39. Combination Sum
  12. (Medium) Leetcode #40. Combination Sum II
  13. (Medium) Leetcode #216. Combination Sum III
  14. (Medium) Leetcode #131. Palindrome Partitioning
  15. (Medium) Leetcode #117. Letter Combinations of a Phone Number
  16. (Medium) Leetcode #93. Restore IP Addresses
  17. (Medium) Leetcode #2375. Construct Smallest Number From DI String
  18. (Medium) Leetcode #2178. Maximum Split of Positive Even Integers
  19. (Medium) Leetcode #1239. Maximum Length of a Concatenated String with Unique Characters
  20. (Medium) Leetcode #1219. Path with Maximum Gold
  21. (Medium) Leetcode #79. Word Search
  22. (Hard) Leetcode #51. N-Queens
  23. (Hard) Leetcode #52. N-Queens II
  24. (Hard) Leetcode #37. Sudoku Solver
  25. More on Leetcode #backtracking