This tutorial is a part of the Data Structures and Algorithms class:
- Typical problems solved by Bellman-Ford algorithm
- Longest path with Bellman-Ford algorithm
- The importance of finding longest, shortest paths
- Summary
Typical problems solved by Bellman-Ford algorithm
- Single source shortest/longest path: find shortest/longest path from a source node to all other nodes in the graph. Simple, Mathematically proven.
- I. When to use: shortest/longest path, also works with negative edges.
- II. Conditions to use: shortest path: NO Negative cycle, longest path: No Positive cycle.
- III. How to use: get the edges, then relax them v-1 times (v is the number of vertices).
- Relaxation shortest path:
if (d[u] + c(u,v) < d[v]) then d[v] = d[u] + c(u,v) - Relaxation longest path:
if (d[u] + c(u,v) > d[v]) then d[v] = d[u] + c(u,v)

lecture-29/shortest-path-bellman-ford.js
// Shortest path, Bellman-Ford
// NO NEGATIVE weight cycle in graph is a MUST
const graph = [
[[1, 4], [3, 5]], // node 0, index 0
[[4, 7]], // node 1, index 1
[[1, 3]], // node 2, index 2
[[2, -10]], // node 3, index 3
[], // node 4, index 4
]
// graph contains NEGATIVE weight cycle
const graphWrong = [
[[1, 4], [3, 5]], // node 0, index 0
[[4, 7], [3, 6]], // node 1, index 1
[[1, 3]], // node 2, index 2
[[2, -10]], // node 3, index 3
[], // node 4, index 4
]
const shortestPathBellmanFord = (graph, sourceIdx) => {
// STEP 1: transform graph from adjacency list to Vertices + Edges lists
const vertices = []
const edges = []
for (let i = 0; i < graph.length; i++) {
// list of node indices
vertices.push(i)
// list of edges [from node, to node, weight]
for (let j = 0; j < graph[i].length; j++) {
const [toNode, weight] = graph[i][j]
edges.push([i, toNode, weight])
}
}
console.log('vertices:', vertices)
console.log('edges:', edges)
// STEP 2: build initial result map
const result = {}
for (let i = 0; i < vertices.length; i++) {
if(vertices[i] == sourceIdx) {
result[i] = 0
continue
}
result[i] = Infinity
}
console.log('result:', result)
// STEP 3: relax the edges n-1 times
const relaxTimes = vertices.length - 1
for (let i = 0; i < relaxTimes; i++) {
for (let j = 0; j < edges.length; j++) {
const [fromNode, toNode, weight] = edges[j]
const newVal = Math.min(result[fromNode] + weight, result[toNode])
console.log(`relax (${fromNode},${toNode}), val old: ${result[toNode]}, new: ${newVal}`)
result[toNode] = newVal
}
}
return JSON.stringify(result, null, 4)
}
const sourceIdx = 0
console.log(`Shortest path Bellman-Ford from node ${sourceIdx}:`, shortestPathBellmanFord(graph, sourceIdx))
// console.log(`Shortest path graph has NEGATIVE cycle ${sourceIdx}:`, shortestPathBellmanFord(graphWrong, sourceIdx))$ node shortest-path-bellman-ford.js
vertices: [ 0, 1, 2, 3, 4 ]
edges: [ [ 0, 1, 4 ], [ 0, 3, 5 ], [ 1, 4, 7 ], [ 2, 1, 3 ], [ 3, 2, -10 ] ]
result: { '0': 0, '1': Infinity, '2': Infinity, '3': Infinity, '4': Infinity }
...
Shortest path Bellman-Ford from node 0: {
"0": 0,
"1": -2,
"2": -5,
"3": 5,
"4": 5
}Longest path with Bellman-Ford algorithm
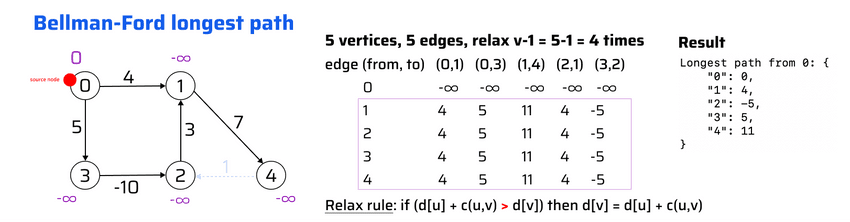
lecture-29/longest-path-bellman-ford.js
// Longest path, Bellman-Ford
// NO POSITIVE weight cycle in graph is a MUST
const graph = [
[[1, 4], [3, 5]], // node 0, index 0
[[4, 7]], // node 1, index 1
[[1, 3]], // node 2, index 2
[[2, -10]], // node 3, index 3
[], // node 4, index 4
]
// graph contains POSITIVE weight cycle
const graphWrong = [
[[1, 4], [3, 5]], // node 0, index 0
[[4, 7]], // node 1, index 1
[[1, 3]], // node 2, index 2
[[2, -10]], // node 3, index 3
[[2, 1]], // node 4, index 4
]
const sourceIdx = 0
const longestPathBellmanFord = (graph, sourceIdx) => {
// STEP 1: transform graph from adjacency list to Vertices + Edges lists
const vertices = []
const edges = []
for (let i = 0; i < graph.length; i++) {
// list of node indices
vertices.push(i)
// list of edges [from node, to node, weight]
for (let j = 0; j < graph[i].length; j++) {
const [toNode, weight] = graph[i][j]
edges.push([i, toNode, weight])
}
}
console.log('vertices:', vertices)
console.log('edges:', edges)
// STEP 2: build initial result map
const result = {}
for (let i = 0; i < vertices.length; i++) {
if(vertices[i] == sourceIdx) {
result[i] = 0
continue
}
result[i] = -1 * Infinity
}
console.log('result:', result)
// STEP 3: relax the edges n-1 times
const relaxTimes = vertices.length - 1
for (let i = 0; i < relaxTimes; i++) {
for (let j = 0; j < edges.length; j++) {
const [fromNode, toNode, weight] = edges[j]
const newVal = Math.max(result[fromNode] + weight, result[toNode])
console.log(`relax (${fromNode},${toNode}), val old: ${result[toNode]}, new: ${newVal}`)
result[toNode] = newVal
}
}
return JSON.stringify(result, null, 4)
}
console.log(`Longest path Bellman-Ford from node ${sourceIdx}:`, longestPathBellmanFord(graph, sourceIdx))
// console.log(`Longest path graph has POSITIVE cycle ${sourceIdx}:`, longestPathBellmanFord(graphWrong, sourceIdx))$ node shortest-path-bellman-ford.js
vertices: [ 0, 1, 2, 3, 4 ]
edges: [ [ 0, 1, 4 ], [ 0, 3, 5 ], [ 1, 4, 7 ], [ 2, 1, 3 ], [ 3, 2, -10 ] ]
result: {
'0': 0,
'1': -Infinity,
'2': -Infinity,
'3': -Infinity,
'4': -Infinity
}
...
Longest path Bellman-Ford from node 0: {
"0": 0,
"1": 4,
"2": -5,
"3": 5,
"4": 11
}The importance of finding longest, shortest paths
- Bellman-Ford lists all possible shortest/longest paths. It's a "brute force" way.
- Math proven means the algorithm guarantees the correct result.
- It's crucial for optimization type 1 and type 2 problem: Maximization, Minimization.
- Bellman-Ford is a proven procedure, too easy so it's rarely asked in coding interview.
- But it's very important for our thinking process. That is if we can present our a problem in form of a graph, it's guaranteed to find max or min. And we can (almost) always present a problem in form of a graph.
| Problem | BFS | Bellman-Ford |
|---|---|---|
| Shortest path (equal edges) | ✅ O(n) |
✅ O(E*V) |
| Shortest path (UN-equal edges) | ❌ | ✅ O(E*V) |
Summary
| Prob. class | P. sub-class | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|---|
| (almost) ANY problem class | array, matrix, ... | Brute Force | O(n) & up |
|
| Can try with any problem type | - pass split test - array, string or graph, ... - divide, solve, combine gives a possible solution |
Divide and Conquer | O(nlogn) |
|
- accessing 2 data points at a time is useful- closing in the pointers proven to give a correct answer - usually array or string |
Two Pointers | O(n) |
||
| 1. Maximization 2. Minimization |
array, string or graph, ... | Greedy choice, no guarantee for most optimal solution |
varies |
|
| - graph or present problem with graph | Bellman-Ford | O(E*V) |
||
| 3. Find all options | array, matrix, ... | Brute Force | O(n) & up |
|
| 4. Find most optimal solution | - shortest/longest path - Min/max |
- graph or present problem with graph | Bellman-Ford | O(E*V) |
| 5. Find a truth | search for a number | - sorted array or balanced BST |
Binary Search | O(logn) |
| accessing a few consecutive data points at the same time is necessary/useful | - usually array or string | Slding Window | O(n) |
|
| - shortest path, equal edge weight - node visitation layer by layer |
- graph or matrix | Breadth First Search | O(n) |
|
| - think top down, think bottom up - node visitation go full depth first |
- graph or matrix | Depth First Search | O(n) |
|
| - what must be done first? | - graph or present problem with graph | Topological Sort | O(n) |
|
| - shortest/longest path | - graph or present problem with graph | Bellman-Ford | O(E*V) |
|
Real life interview questions
- How does Bellman-Ford solve problems?
- What kind of problems can typically be solved by Bellman-Ford?
- Recalculate the Complexity of the problems above.
- Redo the problems above. You should be able to quickly explain how the algorithm works and implement each of them within 15 mins.
- How can we use Bellman-Ford to detect if graph has cycle? Write the algorithm and what is your algorithm's' complexity?
- (Medium) Leetcode #743. Network Delay Time
- (Medium) Leetcode #787. Cheapest Flights Within K Stops
- (Medium) Leetcode #1631. Path With Minimum Effort
- (Medium) Leetcode #1514. Path with Maximum Probability
- (Medium) Leetcode #1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance
- (Hard) Leetcode #1928. Minimum Cost to Reach Destination in Time
