*Prerequisite: Depth First Search.
This tutorial is a part of the Data Structures and Algorithms class:
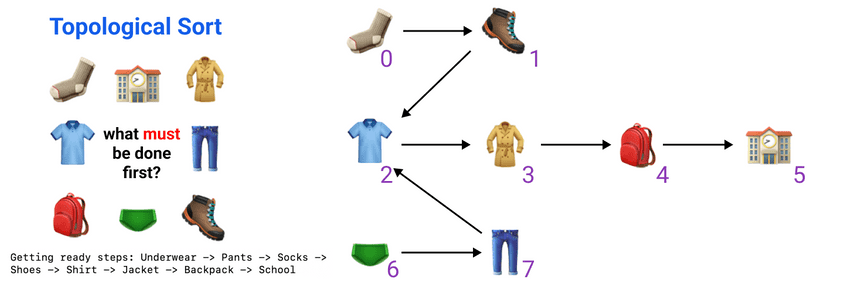
What is Topological Sort?
- Topology: can be thought as whatever you do, structures and relationship are unchanged.
- Topological Sort: sorting without changing existing relationship. Simple, Mathematically proven.
- I. When to use: what must be done first?
- II. Conditions to use: relationship of works is presented in a Directed Acyclic Graph (DAG).
- III. How to use: do a DFS for the all nodes, then reverse the order.
lecture-28/topological-sort.js
// Topological Sort - steps to get ready for school
// step 1: build the graph:
// relationship between what should be done first
// NO cycle in graph is a MUST
const graph = [
[1], // Socks, index 0
[2], // Shoes, index 1
[3], // Shirt, index 2
[4], // Jacket, index 3
[5], // Backpack, index 4
[], // School, index 5
[7], // Underwear, index 6
[2], // Pants, index 7
]
// nodes' information
const idxToItem = {
'0': { name: 'Socks' },
'1': { name: 'Shoes' },
'2': { name: 'Shirt' },
'3': { name: 'Jacket' },
'4': { name: 'Backpack' },
'5': { name: 'School' },
'6': { name: 'Underwear' },
'7': { name: 'Pants' },
}
// topological sort (DFS then reverse)
const topoSort = (graph) => {
const seen = new Set()
let result = []
const dfs = (initNodeIdx) => {
const stack = [initNodeIdx] // REMEMBER to use a proper stack data structure IRL
const temp = []
while(stack.length > 0) {
const curNodeIdx = stack.pop() // pop the stack
// if we've never seen this node before, process,
// otherwise, ignore the node
if(!seen.has(curNodeIdx)) {
seen.add(curNodeIdx) // add this node to seen list
const curNodeNeighbors = graph[curNodeIdx] // get the neighbors
curNodeNeighbors.forEach(nodeIdx =>
!seen.has(nodeIdx) && stack.push(nodeIdx)) // push neighbor on top
temp.push(idxToItem[curNodeIdx].name) // save current node to temp
}
}
result.push(temp)
console.log('result: ', result)
}
// make sure every single node is visited
for(let i = 0; i < graph.length; i++) {
if(!seen.has(i)) dfs(i)
}
// Reverse
result.reverse()
console.log('result after reverse: ', result)
return result.flat().join(' -> ')
}
console.log('Getting ready for school:', topoSort(graph)) // Underwear -> Pants -> Socks -> Shoes -> Shirt -> Jacket -> Backpack -> School$ node topological-sort.js
result: [ [ 'Socks', 'Shoes', 'Shirt', 'Jacket', 'Backpack', 'School' ] ]
result: [
[ 'Socks', 'Shoes', 'Shirt', 'Jacket', 'Backpack', 'School' ],
[ 'Underwear', 'Pants' ]
]
result after reverse: [
[ 'Underwear', 'Pants' ],
[ 'Socks', 'Shoes', 'Shirt', 'Jacket', 'Backpack', 'School' ]
]
Getting ready for school: Underwear -> Pants -> Socks -> Shoes -> Shirt -> Jacket -> Backpack -> SchoolTypical problems solved by Topological Sort algorithm
Identify the nodes, construct the graph.
- Course schedule problem.
- Dependency resolution.
- Operation system deadlock detection.
- Finding cycle in graph.
- ...
- Any problem with relationship and what must be done first.
Summary
| Prob. class | P. sub-class | Input characteristics | Algorithm | Time Complexity |
|---|---|---|---|---|
| (almost) ANY problem class | array, matrix, ... | Brute Force | O(n) & up |
|
| Can try with any problem type | - pass split test - array, string or graph, ... - divide, solve, combine gives a possible solution |
Divide and Conquer | O(nlogn) |
|
- accessing 2 data points at a time is useful- closing in the pointers proven to give a correct answer - usually array or string |
Two Pointers | O(n) |
||
| 1. Maximization 2. Minimization |
array, string or graph, ... | Greedy choice, no guarantee for most optimal solution |
varies |
|
| 3. Find all options | array, matrix, ... | Brute Force | O(n) & up |
|
| 4. Find most optimal solution | ||||
| 5. Find a truth | search for a number | - sorted array or balanced BST |
Binary Search | O(logn) |
| accessing a few consecutive data points at the same time is necessary/useful | - usually array or string | Slding Window | O(n) |
|
| - shortest path, equal edge weight - node visitation layer by layer |
- graph or matrix | Breadth First Search | O(n) |
|
| - think top down, think bottom up - node visitation go full depth first |
- graph or matrix | Depth First Search | O(n) |
|
| - what must be done first? | - graph or present problem with graph | Topological Sort | O(n) |
|
Real life interview questions
- How does Topological Sort solve problems?
- What kind of problems can typically be solved by Topological Sort?
- Recalculate the Complexity of the problems above.
- Redo the problems above. You should be able to quickly explain how the algorithm works and implement each of them within 15 mins.
- Redo example above with Loop.
- You can start Topo sort from any node. Redo the example above starting with node 3. Update the code accordingly to make sure all nodes are visited. What do you think about the result?
- (Medium) Leetcode #207. Course Schedule
- (Medium) Leetcode #210. Course Schedule II
- (Hard) Leetcode #2392. Build a Matrix With Conditions
- More on Leetcode #topological-sort.
